
Use your browsers find function (ctrl f) to search for your key word.
Outline
This page is designed to connect educators and others to a comprehensive mathematical knowledge base, to enrich pedagogical skills and facilitate mathematical literacy. Information is meticulously organized into three main categories and technology:
Mathematical knowledge base of concepts & outcomes
Content dimensions
Number value & operations
- Activities - Problems, units, packets ... for Number value & Operations (+, -, *, & /)
- Pedagogy - Related to Number value & Operations (+, -, *, & /)
Algebra, Patterns, Ratio, & Proportion
- Activities - Problems, units, packets ... for Algebra, Patterns, Ratio, & Proportion
- Pedagogy - Related to Algebra, Patterns, Ratio, & Proportion
Geometry & Visual spatial reasoning & representation
- Activities - Problems, units, packets ... Geometry
- Pedagogy - Related to Geometry & Visual spatial reasoning & representation
Data Analysis & probability
- Activities - Problems, units, packets ... Data Analysis & Probability
- Pedagogy - Related to Data Analysis & Probability
Measurement
- Activities - Problems, units, packets ... Measurement
- Pedagogy - Related to Measurement
Process dimensions
Problem solving, Reasoning and proof, Representations, Communication, & Connections
- Pedagogy - Problem solving, Reasoning and proof, Representations, Communication, & Connections
- Activities - Organized by mathematical dimensions
Last edited - February 25, 2026

Knowledge base & pedagogical tools for mathematical literacy
Knowledge base outline of concepts
The mathematical knowledge base includes concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come. Includes
concepts, outcomes, & vocabulary by content, processes, and attitudinal (values & dispositions) dimensions by levels.
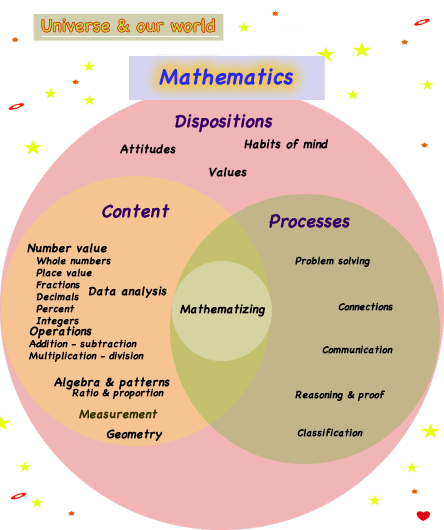
- Algebra & patterns
- Attitudinal (disposition & value statements)
- Classification
- Communication
- Connections & perspectives
- Data Analysis & Probability
- Geometry
- Measurement & measurement estimation
- Number value
- Operations & computation estimation
- Problem solving
- Reasoning & proof
- Relative Position and Motion
- Variable
Pedagogical knowledge to facilitate mathematic's literacy & develop professionally to create learning experiences to facilitate mathematical literacy
The fields of mathematics map & explanation video (11:05)
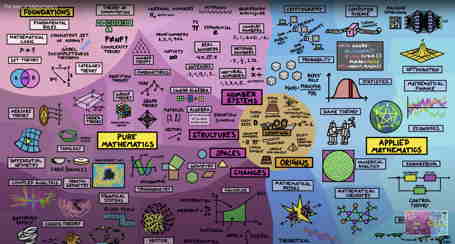
Resources for professional development
- General information for all professional educators to create a professional educator conceptual framework & knowledge base
- Procedure for professional mathematics educators development - information to create a professional mathematics educator conceptual framework & knowledge base
- Definitions of mathematics and focus questions to analyze them
- Development of reasoning and logical thinking across ages
- Mathematical vocabulary lists by dimensions & levels - to review when planning learning activities
- Kinds of numbers - fact sheet
- Books
- Activity to explore conceptual & procedural knowledge - Illustrated with card trick - magic video ...
- Supporting research on the importance for mathematics teachers to combine conceptual & procedural
- Kappan. Beyond the Math Wars: the importance of knowledable mathematics teachers.pdf. By Rachel S. McClam, Rebecca A. Cruz. Dec 2, 2024.
- Kappan. The Politics of California School Mathematics: The Anti-Reform of 1997-99.pdf by Jerry P. Becker and Bill Jacob, Vol. 81, No. 7 (Mar., 2000), pp. 529-532, 534-537
- Kappan, The Mathematical Miseducation of America's Youth: Ignoring Research and Scientific Study in Education.pdf. by Michael T. Battista, February 1999.
- Supporting research on the importance for mathematics teachers to combine conceptual & procedural
- Considerations for Planning to Teach: Big ideas, concepts, & generalizations all subjects
- Hands on - What is it really? pretest, from concrete to abstract, Bruners instructional modes, touch math
- History of mathematics in North America
- Independent study: planning guide to help select and refine topics
- Memory: learning basic facts & algorithms - getting learners to slow down & think, making better choices on how to proceed
- Mental math quiz to compare traditional algorithmic solutions to non traditional algorithmic solutions mathematicians are likely to use
- Misunderstood mind - video & information on PBS
- Principled procedures for Math Educators
- Quizzes
- Teaching & learning - Mathematical practices and research, Survey your current understanding of teaching and learning mathematics, then compare your thoughts with what current research suggests.
- down & think, making better choices on how to proceed
- Mental math quiz to compare traditional algorithmic solutions to non traditional algorithmic solutions mathematicians are likely to use
- Reflecting on mathematical instructional practice - suggestions to reflect beyond a summary of what happened
- Sample outline with suggestions for creating a professional portfolio
- Teaching & learning - Mathematical practices and research, Survey your current understanding of teaching and learning mathematics, then compare your thoughts with what current research suggests.
- Visual & Spatial Representations - Modes of visual learning, literacy, & research, suggestioins & activities
Planning resources
General planning
Planning information
- General instructional theory - explanation with examples flexible enough to plan any topic & intended learning
- Overview for planning and creating curriculum documents
- Outline for a year plan and suggestions
- Outline for a sequence or unit plan with suggestions
- Sample number talk outcomes for 16 & math conference outline
Examples to prep intended learnings
- Framework with explanations of mapping categories for planning to teach big ideas, concepts or generalizations
- Blank planning map
- Classification sample planning map
- Equality and equal arm balance
- Geometry, Area sample planning map
- Proof and reasoning sample planning map
- Thoughts about math games, competitions, and simulations
- Literature to teach math - Includes - uses of literature to facilitate math literacy, ways to mathematize literature, list of literature books with mathematical themes, literature suggestions by math dimensions, sample lessons using literature books
Suggestions for selecting problems and investigations
- Problem solving - How to solve problems, heuristics, strategies, teacher's role in problem solving, suggestions to help learners solve problems, sample questions to assess learners' mathematical problem solving, scoring guides and rubrics, characteristics of a good problem ideas to consider when writing or selecting problems. planning questions to prepare to facilitate problem solving & investigating suggestions to consider when writing or planning to use problems, problem solving goals and outcomes to review for the inclusion in appropriate curricular documents and plans, problem solving vocabulary to introduce to learners, dispositions to review & select to focus on.
Sample parts and pieces of sequence plans
- Sequence plan with activities to build to cardinality - Good start with multiple concepts, sequence of concepts, and very good lists of activities for concepts. Need more integration of mathematical dimensions for practice of mathemtics and scoring guides with levels.
- Sequence plan for measurement, data analysis, and rounding - Uses body measurements to explore proportions. Integrates mathematical dimensions of number value (rounding,), algebra (proportion), measuring, graphing, scaling, data analysis (categorical data) to suggest integrated mathematical practices. An outline and could use editing for clarity and more depth.
Sample activity plans
- Card trick | Includes integration of mathematical dimensions, good for proof, could use some editing for clarity card trick demonstration with different instructional strategies [conceptual & procedural].
- Reading and writing numbers with numeral and words | Good activity for skill building and necessary skill, doesn't include integration of mathematical dimensions,
- Estimating chocolate chip | Has potential, but needs a lot more information for integration of mathematical dimensions and extended activities.
Assorted tools
- Characteristic of mathematically talented & development of talent
- Mathematics & Logic adapted Frayer Model
- Manipulative materials list
- Math review game - Includes questions with hints, answers, & study resources. Excellent to use to tutor all middle level learners.
- Parent letter for using manipulatives and representation with multiplication & division
- Parent involvement - Suggestion for parent and community involvement.
- One activity to get involvement is a math night. Which can be organized by selecting from activities you use in your curriculum. Many are included on this page. Children and adults enjoy playing games and solving problems.
- Eight different uses of literature for teaching mathematics
- Annotated list of literature and classroom uses in NCTM Journals
- Mathematical terms and their representations with Cuisenaire Rods
- Investigations with Cuisenaire rods & student worksheets
- Comparison or English - Spanish wording in math. Translations of some mathematical ideas . Notice how some are the similar and others are very different. Demonstrates that direct translation is generally not as simple as one thinks unless one is bilingual.
- Math Their Way notes
Assessment
- Assessment introduction and review: [ Suggestion for creating criteria referenced assessments ] [ Norm-referenced test information ]
- Letter to parents for student lead conferences and authentic assessment
- Questions from standardized achievement tests . SAT, FAA, MCAT, ...
- PISA 2012 Problem-Solving sample questions
- Curriculm Documents with concepts, outcomes, and assessment levels
Sample assessments
- Student survey - open ended about student's math practice - one page
- Student survey - rating sheet (always, mostly, some, not) - about two page
Curriculum
- Comparison of dimensions and categories of NCTM and CCSS of math
- Concepts, suggested sequences, plans, rubrics, and other stuff may be found linked at the top of the page in mathematics content.
- Standards
- Curriculm Documents with concepts, outcomes, and assessment levels
- Rubrics click the desired mathematics dimensions at the top of the page to locate concepts... assessment... evaluation ...
- Notes on exemplary and promising math programs
Workshops, courses, tutorials
- ESU #1 Algebra Workshop information
- Information for graduate Class or professional development
- Information for preservice Class or professional development
- Videos for professional development
- Technology Help Pages - ILife and Windows Media tutorials and help pages for using/ making: photos, audio, and video --->>> directions and tutorials...
- NATM fall conference presentation 2006
- NATM spring conference presentation 2005
- NCTM regional presentation fall 2004

Numbers: values and basic operations
Knowledge base & tools to develop mathematical literacy
Knowledge base
Mathematical knowledge base with concepts necessary for learners to conceptualize to become mathematically literate and misconceptions that must be over come. Particularly important for how learners develop their understanding of numbers, their values, operations, patterns, and relationships are:
Concepts related to number sense:
- Number sense
- Classification - children must know how to classify to determine groups (sets) to count & determine number values. More advanced classification ideas are needed to compare number values.
- Whole numbers
- Addition and subtraction
- Place value
- Multiplication & division
- Fractions
- Decimals
- Percents
Information to facilitate literacy in numbers (values & basic operations) & tools to achieve it
Numbers & their definitions - Fact sheet of natural, integer, rational, irrational and real numbers. Their definitions, examples, & number line visual representation.
Vocabulary lists related to number sense
- Number sense & operations
- Vocabulary for operations by grade levels
- Operations
- Fractions
Numbers: Counting, recognition, cardinality
- Prenumber sense (birth - 6/8 years) - beginning development of number sense
- Conservation - development of conservation of number & other reasoning tasks
- Subitizing before counting - development of subitizing before accurate counting
- Counting - overview of the development of pre counting to number sense & hierarchial inclusion
- Recognizing & writing numbers .pdf booklet - simulation to recognize problems some learnes may have developing this fluency.
- Skip & choral counting - instructional suggestions with examples
- Skip & choral counting by three-fifths - example with worksheets
- Whole Number value (6/8 years & beyond) - development of number value after number conservation & one-to-one correspondence to hierarchial inclusion
- How to say, read, & write numbers from billion to billionths - lesson plan & worksheets
- Framework for planning counting and cardinality units
- See also place value development
Assessment of development
- 13 Whole number assessment tasks - Scripts, materials, scoring guides, and Summative record sheet for all , K-2.
- Counting with synchrony or one-to-one correspondence & cardinality [ Synchrony information] - script with materials, problems, suggestions & scoring guide
- Rote counting to 100 - script with problems, suggestions & scoring guide
- Writing numerals 1-9 - mnemonic phrases to teach to help students remember how to form numerals and assessment script with scoring guide.
- Rote counting by multiples, 2, 5, 10, & 3 - script with materials, problems, suggestions & scoring guide
- Counting back from 10, 20, 100 - script with materials, problems, suggestions & scoring guide
- Counting to and from 1 000 . - script with materials, problems, suggestions & scoring guide
Counting to 0ne-thousand requires memory of the necessary words, but also a conceptual understanding of ten repeated 100's. - Numeral recognition - (1-20) with worksheet, script, suggestions & scoring guide
- Number recognition - prompt sheets (numerals 1-10, & 10-20 randomly arranged) & directions
- Writing or forming numerals - script with materials, problems, suggestions & scoring guide
- Subitizing or instant recognition of values - script with materials, problems, suggestions & scoring guide
- Assessment for One-to-one correspondence with matching - script with materials, problems, suggestions & scoring guide
- Cardinality matching - subitizing or visual pattern recognition, script with materials, problems, suggestions & scoring guide
- More or less - script with materials, problems, suggestions & scoring guide
- Cardinality match numeral and number word - script with materials, problems, suggestions & scoring guide
- Hierachial inclusion to five - script with materials, problems, suggestions & scoring guide
- Cardinal scoring guide and rubric
- Conservation tasks - six conservation of number tasks with instructions, developmental notes, & possible outcomes
Place value development & assessment
Development
- Place value - development from age 5 on: ten as big number, group by ten, pre place value, unitize, place value relationships, decimals, exponents, place value & decimal worksheets
Assessment
Fractions & ratio development & assessment
Development
- Development of fractional number values , instructional ideas, sample activities, worksheets, and assessment. Focus is on the development of fractions as equal parts of a whole, sub groups, & equivalent fractions and decimal fractions. Worksheets include: fraction circles, circle disks, paper folding, area models, measurement models, number lines, hundred charts, challenges, & problem suggestions.
- Fractions, decimals, percent - development of fractions, decimals, percent and their operations, and connections
- Whole numbers, fractions, rational & irrational numbers, infinity, & number lines - instructional notes
- Fractional value & equivalency - scoring guide suggestions & rubric
Operations
Addition & subtraction - whole number development & assessment
Development
- Addition & subtraction - development of addition and subtraction as operations and ways to assess it. Includes an analysis of the four types of addition & subtraction problems - chart with multiple examples for the three subtypes of all four types
- Memory, learning, and developing skill with basic facts & dot plates
- Dot plates
- Strategies for addition & subtraction - includes instructional suggestions and sequences to help develop people's ablity to solve addition and subtraction problems mentally.
Assessment
- Addition and Subtraction - suggestions, directions with problems, scoring guides, & score sheets to assess the development of + & - from four ways: join, separate, part-part-whole, & combine with scoring guide ideas to understanding and use of algorithms
Multiplication & division of whole number development & assessment
Development
- Multiplication & division - development of understanding and strategies
- Development of multiplication facts
Addition, subtraction, multiplication, & division - fractional numbers development & assessment
- Addition and subtraction sequence
- Story problems with representational starters for addition of fractions with unlike denominators thanks Brant
- Multiplication and division sequence
Division problems represented with squares and rectangles
- Sample problems : 1/2 ÷ 1/2, 1/2 ÷ 1/4 , 1/2 ÷ 3/4, 1/2 ÷ 3/5 (thanks Brant),
- Division problem (5 8/10 ÷ 5) with eight different solutions
- Multiplication of fractions with Cuisenaire Rods explanation how to multiply
- Division with 12 & 4, & the importance of problem diversity
Addition, subtraction, multiplication, & division - decimal numbers development & assessment
Activities to facilitate number values, & operations literacy
Number sense - whole numbers
- 100's of Instructional ideas and activities for number sense & place value

- Counting and cardinality Lesson plan - review also as a planning framework
- Bean toss directions and Fold book patterns for tossing 1-10 beans
Number relationships --->>> see patterns and algebra
Dot plates & subitization: activities
- Dot plates video and explanation about memory, number value, and basic facts
- Eight dots in one pattern with different interpretations
- Subitize information & resources
Manipulatives for students to use to learn number value

Cards for learners to sort - make a set of cards by combining cards appropriate for a particular learner: numerals, words, ordinal, dot, ten frame with dots. The cards can be sorted into paper bags, a sorting box, or on any flat surface. Different games or activities can be created: sort dots, sort dots and label with the set's cardinality numeral word, sort and label with ordinal word, sort all cards and beat the clock ...
Sample cards to print and cut out :

- Blank cards
- Numerals 0 - 9
- Number words zero - ten
- Ordinal words first - tenth
- Dot cards:
- Ten frame cards

Dice game - helps students subitize number value and introduction to addition. Roll the dice and flip the values on the die or the sum of the die. Continue to roll until all the numbers (1-12) are flipped (win) or a value rolled has had all it's possible plays, already flipped. Example: roll 2 & 2. Can flip 4, or 1 & 3.
Die roll - simulate a roll of a die .
Number talks: are good tools to show equality of numbers and different ways to represent the same values. Sample number talk outcomes for 16 & math conference outline.
Number line : is a good mathematical tool to represent mathematical values and operations. However, children who are not familiar with them and confident with their use, are not sure what to count: numbers, lines, spaces and where to start (0, 1, ...).
Therefore, before they’re used as a representation to explain and prove mathematical ideas, learners need experiences to develop their understanding and fluency with their use.
Activities, used when counting, such as numbered polka dots organized in a line can provide good background before introducing a number line. ![]()
- Introduction to a number line
- Number line - place values from billions to billionths
- Numbers listed - in order from billions - billionths
- Add-on or count-back
Place value - whole numbers & decimal numbers
Manipulatives for multiples of 10 and 100
- Blank ten strip
- Page of 10 blank ten frames
- Ten and more (teen numbers) Fold Book
- Ten and more (teen numbers) worksheet
- Blank twenty strip
- Hundred chart
- Upward hundred chart
- Zero to 100 chart
- Blank hundreds frame four 10 cm squares.
- Blank hundred chart larger
- Thousand chart
- Hundred chart puzzles and puzzle pieces puzzles
- Number line - place values from billions to billionths
- Numbers listed - in order from billions - billionths
Really big numbers and infinity
- Olber's Paradox - if the universe is infinite in time and space, stars should occupy every point in space and fill the night sky with light.
- How many grains of sand in the Universe? Archimedes' proof in The Sand Reckoner.
Number Theory
Number theory is critical for students to do well in algebra and higher levels of mathematics. However, the sad thing is most teachers are unfamiliar with these ideas, or skip them when they occur in their math text or program, as their view of mathematics is limited to basic facts and operations as calculations of numbers.
The following are examples related to number theory.
- Using primes to find common factors, multiples, LCM and GCF ALL together
- Sample dialogue that explores a learners conjecture about multiples and moves to primes and then to the fundamental theory of arithmetic (FTA) ...
- | Factors of first 50 & 100 notes | Factors to 100 chart |
- The Fundamental Theory of Arithmetic
- Fibonacci sequence
- Patterns with a factor & a constant factor to find a function - relates to casting out nines
Fractions, Decimals, & Percents number values
- Fractions - development of fractional number values, instructional ideas, sample activities, workheets, and assessment. Focus is on the development of fractions as equal parts of a whole & equivalency. Worksheets include: fraction circles, circle disks, paper folding, area models, measurement models, number lines, hundred chart, challenges, & problem suggestions.
- Fractional parts of a subdivided square Challenge - Worksheet to find & record halves, fourths, eights, & sixteenths of a square with inscribed shapes
- Fractions - Worksheet to represent 1/2, 1/4, 1/8, 1/16, 1/32 on a number line
- Fractions - Worksheet to explore the fraction 3/5 with skip or coral counting & its patterns
- Fractional values compared problems
- Using fractions to find the area of nine shapes in a 17 square unit rectangle - The Pharaoh's problem
- Percentage - sample activities and worksheets
- Ratio and Fraction values problems (ratio is relationship between two or more quantities.)
- Sequences
- Number line with whole & decimal numbers - place values from billions to billionths
- Numbers for whole & decimals - in order from billions - billionths
- Decimals either end in zero or repeat as nonterminating decimals or rational numbers.
Example: place these numbers on number line 1, 2/3, .5, .3 , 1 1/2, 2, .6 , 1/2, .9 , 1 .1 , 1/3 Misconception .9 doesn’t equal 1. Recognize 1/3 = .3 & 2/3 = .6 . but not .9 = 1.0
Basic Operations (+-*/)
Addition and subtraction whole numbers (+ -)
- Transitional activities from number sense to addition and subtraction
- Sample subtraction algorithmic solutions
- Addition facts table
- Add on or count back - in comic form
- Bucket problems application of addition, subtraction, problem solving, combinations, reasoning.
- Magic triangle
- Magic square perimeter
Multiplication and division of whole number (* /)
- Multiplication arrays Molly B
- Area model for multiplication & to develop a traditional multiplication algorithms and its connection to algebra -> two examples -> two digit numbers example -> a couple of reasons why this is an important representation related to algebra & for two digit multiplication
- Multiplication facts table
- Representations of 21 / 7 or π.
Fractional numbers (+ - * /)
Activities for number sense particularly: fractions, decimals, and percents
- Addition and subtraction sequence
- Story problems with representational starters for addition of fractions with unlike denominators thanks Brant
- Multiplication and division sequence
Division problems represented with squares and rectangles
- Sample problems : 1/2 ÷ 1/2, 1/2 ÷ 1/4 , 1/2 ÷ 3/4, 1/2 ÷ 3/5 (thanks Brant),
- Division problem (5 8/10 ÷ 5) with eight different solutions
- Multiplication of fractions with Cuisenaire Rods explanation how to multiply
Decimal numbers (+ - * /)
Activities for number sense particularly: fractions, decimals, and percents
Integer values and operations (+ - * /)
Addition and subtraction of positive and negative integers might be conceptualized by representing and controling two properties: position on a number line and direction of body.
The number line can have two halves with the same numbers being both positive and negative. You have two choices for each number + or - as a reference to position. If the number has a value of 4, it could be represented as a positive four or negative four.
You can represent those two numbers by standing on either +4 or -4. Secondly when you are standing on a number line you can face one of two direction, since the number line is bidirectional, you might be facing left or right, forward or backward, in a positive direction or negative direction. or if it is thought of as a thermometer, you can walk hotter or colder.
Problems can be posed as :
Find a starting point, say -3 and if you add a +3, face warmer and walk forward 3.
Find a starting point, say -3 and if + -3, then face warmer and walk backward.
Find a starting point, say -3 and if - - 3, then face colder and walk backward.
Find a starting point, say -3 and if - +3, then face colder and walk forward.
Again both are important and a concrete model can be used to describe a procedural rule, as demonstrated as a plus and a plus are plus, a plus and a minus are a minus, and a minus and a minus are a plus.
Another idea is to record a video with motion. People walking or running forward and backward. They might display signs with forward and backward as they do so. However, it probably will be obvious which direction they moving when it is recorded. When the video is made, then each can be viewed with the movie play forward and backward. A chart of the different results can be made (forward, forward, results in forward; forward, backward, results in backward; backward, forward results in backward; backward, backward results in forward.
After several concrete experience have been experienced explore the this challenge.
How many different ways can two numbers be represented with different a sign and an operation (-2 ++3; -2 -+3; -2 --3; -2 +-3) (2 ++3; 2 -+3; 2 --3; 2 +-3).

Algebra Patterns and Functions
Knowledge base & tools to develop mathematical literacy
Knowledge base
Mathematical knowledge base with concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come. Particularly important for how learners develop their understanding for algebra, patterns, and functions are:
Concepts related to:
- Algebra & Patterns
- Ratio & proportion
- Concepts and Outcomes from Science for All Americans (SFAA) & National Assessment for Educational Progress (NAEP)
Information to facilitate literacy in algebra, patterns, & functions & tools to achieve it
- Assessment
- Functions & patterns - Worksheet of a sample of Authentic Assessment for a Bridge pattern
- Functions & patterns - Worksheet of a sample of a Directed Assessment for a Bridge pattern
- Assessment - process proof and conjecture - content zero and properties of zero - addition and subtraction - with teacher reflection
- Scoring guides
- Equality & equal symbol - scoring guide or rubric across levels
- Classification or Sorting - Activities to assess by 1, 2, & 3 properties; use of Venn diagrams to represent intersecting & disjoint groups.
- Conjectures - Articulating, editing, & refining conjectures in a second or third grade class
- Equality and equal sign in equations - Discusses equality, equals symbol, its big ideas, supporting concepts, development, scoring guide, & ideas to facilitate understanding. Includes the use of an equal arm balance to discover equality. With photos and different models made from K'Nex.
- Graphing - Instructional Plan for teaching graphing & solving for two unknowns four ways. (8-12 Grade) graph paper
- Justification & proof with 3 examples: concrete, pictoral, & symbolic levels for odd plus odd is even
- Multiples, common multiples, & FTA - Discussion script includes: least common multiple, the next common multiple, fundamental theory of arithmetic (FTA) see FTA chart in activities
- Primes and composites - Diagram to use to explore the primes of whole numbers 1 - 40 & invent the Fundamental Theory of Arithmetic (FTA)
- Bottle & cork price problem - guess & check, trial & error, later algebra
- Algebra, patterns, & function vocabulary - lists of vocabulary for primary, middle, & upper levels.
- Statistics timeline and history
- Reflections from ESU #1 workshop
Activities to facilitate algebra, patterns, & functions literacy
- Adding consecutive numbers - Worksheet challenge to find a sshort cut to add 4 consecutive numbers, hint, and verification proof.
- Arithmetic Properties - Chart with properties, conjectures, examples, & non examples of numbers and operations: addition, subtraction, multiplication, division, identity, inverse, zero, commutative, & distributive.
- Calendar math problems - List of challenges & hints to identify dates which are: factors, primes, relatively prime, pi, triangle numbers, square numbers, palindromes, perfect number, reciprocals, reciprocal numbers.
- Equality, relationships, & equal arm balances
- Expressions & formulas - Bus, train boarding and deboarding problems for problem solving, expressions & recursive formulas, problem solving strategies of working backwards& acting out.
- Factors - Planning notes, 4 Worksheets: table to list factors 1-50, table to sort factors by least to most for numbers 1-50, table to list factors 1-100, table to sort factors by least to most for numbers 1-100,
- Fibonacci Sequence explanation Slide show that explains the Fibonacci sequence and how to generate it. for generating the sequence & Fibonacci Numbers in Nature First 12 numbers in the sequence .
- Function exploration - includes definitions with examples, diagrams, & representations including a function machine. Also activity with work sheet and charts to explore a function with a variable factor (3) & constant factor (27) & discover casting out nines
- Fundamental Theory of Arithmetic (FTA) - Chart with primes & prime factorization to 30 and blank to 40 to represent the FTA.
- Graph, the math representations behind the modern graph - Story of Nicole Oresme, Father of the modern graph, or as he would say: the Latitude of Forms
- Graphing Notes - Data sheet for coordinate graph, manipulated, responding, independent, dependent, variables, relationships, extrapolation, interpolation, continuous & categorical data (graph paper)
- Use the rate of water flow from a shower head to graph the gallons of water used for a shower from 0-20 minutes. Find how much water is used when taking a bath in a regular and jacuzzi tub. Use the information to decide under what conditions it is better to take a bath or shower to conserve on water.
- The Königsberg bridges problem
- Magic phone number - Solve the magic with an equation. Worksheet Magic explained with math, Inverse properties of numbers & operations.
- Pizza - decide if the pricing of three pizzas 9, 12, & 15 inches are fair or best deal.
- Linear equations - fact sheet for y=mx+b, slope, & y intercept
- Graphing Pictures plots - Worksheet to plot a picture and create your own points to plot. Source Johnnie Ostermeyer
- Growth - plants and the mathematics of growth
- Pattern activities - Investigatons to develop patterns & formulas. Starting with number strips, dot patterns & other growing patterns: v, w, pyramid, prism, tower, triangle, rectangle, log stack, can stack, hand shake, dancers, step pyramid, & disc ...
More ...- Even, odd, and super even patterns exploration and investigation activities
- Categorical sorting - Activities descriptions, Venn diagrams, sort by one, two, three properties, disjoint groups and intersecting groups
- Happy numbers -
- Stairways and stacking blocks problems - Worksheet , also known as odd squares & tower problem
- Sixteen Colored Squares in an Eight by Eight square problem how many?
- Growth - plants and the mathematics of growth patterns
- Petals around the Rose - is a simulation to find a strategy to determine the number of petals around the rose as simulated by dice. Direcctions & hints .
- Probability activities - See data analysis & probability
- M&M's what colors in a package ? - Worksheet Count, chart, determine percentage, mean , median, mode of M&M's in a package by color.
- Multiplication of whole numbers, multiplication of binomials (x+1)(x+1), & area patterns
- Necklace perfectly beaded - Worksheet to identify a perfect beaded necklace repeating pattern & create one
- Primes and composites. A study of whole numbers - Chart with prime factors for 2 - 40 to invent the Fundamental Theory of Arithmetic
- Pythagorean Theorem proof
- Toothpick challenges
- Growing squares challenge - Growing square swith toothpics challenge. Includes picures or slides that step through adding toothpicks to grow squares, record data in a table, to show the pattern of increasing squares and increasing toothpicks.
- Growing squares worksheet - Use toothpicks to find a pattern & formulas to determine the number of toothpicks added to make larger squares. Toothpicks in the perimeter, toothpicks to make the squares in the squares, and the number of squares in the growing squares.
- Toothpicks in a rectangular pattern - Worksheet with hints to write equations for the sums of toothpick patterns in a rectangle and discussion ideas for what is an equation, function, and can they be both.
- Relationships - Pools and sidewalks Worksheet growing squares and perimeter patterns, relationships, & functions.
- Shadows - What is the length of the coaches shadows?
- Simultaneous Equations proofs
- Stem and leaf plot - Worksheet with problems and Java plotter available on the internet
- Variables. One variable activities - ping-pong ball race experiment, collect data, analyze (ping-pong ball race, how many stars in a minute).
Ratio & proportion
Ratio is relationship between two or more quantities that stays the samewhen both quantities are multiplied or divided by the same factor. The relative size is the same when the two quantities are scaled.
Proportion is the equality of two ratios. It emphasizes the relationship between the parts and the whole, ensuring a balanced distribution. Proportions are represented using the = sign, indicating the two ratios are equivalent.
- Jo Tall and Jo Short - Worksheet ratio & proportion activity, historical research problem used to investigate the develop of reasoning as suggessted by Piaget
- Measuring heights of trees & other objects - clinometer, shadows, scale (Biltmore) stick
- Candle problems - Worksheet with sample rate & proportion problem and solution with follow up problem and questions.
- Sack Lunches - Teacher randomly passes out lunches. What are the odds? - Worksheet with hints & discussion ideas.
- Wages for Pet Care
- Acrobats Logic Problem - Worksheet draw a diagram, proportion & problem solving diagrams

Geometry & Spatial reasoning
Knowledge base & tools for mathematical literacy
Geometry originates from Greek ge or gaia meaning earth or land and metria meaning measuring, or measurement of earth or land. Today geometry’s big ideas include the study of spatial properties and relations of points, lines, surfaces, solids, and higher dimensional quantities. Their shapes, variables or invariables, definitions, & proofs.
Analytic geometry is the combination of geometry and algebra.
Relative position is used to locate objects in space with distance and directions.
Knowledge base
Mathematical knowledge base with concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come. Particularly important for geometry and spatial reasoning are:
Tools to facilitate literacy in geometry & spatial reasoning & tools to achieve it
Background information for learning and teaching.
- Spatial and visual representations, abilities, & literacy - article
- Stages of geometric thinking - Pierre and Dina van Hiele' levels of geometric thinking in a chart
- Developmental sequence of geometric ability
- Longitudinal development of volume at the middle level - short article
- Visual and spatial reasoning - article includes visual thinking, related careers, research, skills, perception, memory, creative, six modes of visual learning (developed by the Polaroid Education Program), & instructional activities to develop visual spatial abilities
- Geometry vocabulary - lists of vocabulary for primary, middle, & upper levels.
Activities to facilitate geometry & visual spatial literacy
- Assorted activity suggestions - No Worksheet or detailed explanation: topics include: Volume, Area, Visualization ...
- Area & perimeter assessment - Worksheet with seven direct assessment questions. It defines a hexaright shape, which is used to assess the depth of understanding of area, perimeter and their relationships.
- Area & perimeter - pools and sidewalks - Worksheet patterns, relationships, & functions with area and perimeter
- Cartography map making, angle measurement, compass, clinometer, measure height, distance, locating objects with distance & angle combinations, contour maps, using triangles to measure
- Measuring heights of trees & other objects - clinometer, shadows, scale (Biltmore) stick
- Measuring Earth's circumference, Eratosthenes, astronomy, solstices, equinoxes, latitude, science, and math - Background information & worksheet with instructions to calculate circumference of the Earth on a solstice using angles and distances.
- GPS (Global positioning service) - Current and history of GPS and Cell phone mathematics - The story of how Brad Parkinson who used creativity & mathematics to enable cell phones.
- Metatrons Cube and Platonic Solids - Link to external site
Puzzles & challenges, with worksheets
- Area of nine shapes in a 17 square unit rectangle - The Pharaoh's problem
- Biggest body of water challenge - Select two bodies of water, lakes, rivers, sea, gulf, ocean.. and use their measurements and geometry to document reasoning for why you believe one is bigger than another. Decide how to measure: one dimension, length, width, height, or two dimensions - area, three dimensions volume or four? Time? …
- Broken Square Puzzle 4 pieces - Worksheet to make a square & solution
- Broken Tee puzzle 1 - Worksheet to make a capital T & solution
- Broken Tee puzzle 2 - Worksheet to make another capital T & solution
- Five - five piece puzzles - Classic square and four other shapes, directions, hints, solutions, worksheets and puzzle pieces patterns
- Triangles in the shapes puzzle - Worksheet to find triangles & hints
- Squares & triangles - puzzle, challenge, worksheet to find squares & triangles
- Tangrams - Directions for folding & cutting a square sheet of paper or oak tag to make the Tangrams
- Tangram puzzles - Worksheet to find & record fifteen different geometric shapes made with Tangrams
- Tangrams - Worksheet pattern with Tangram pieces in a square
- Three dimensional puzzles - images and patterns
- Four name word puzzle - Worksheet & puzzle
- Fractional parts of a subdivided square Challenge - Worksheet to find & record halves, fourths, eights, & sixteenths of a square with inscribed shapes
- Pentominoes - Describes Pentominoes shapes, history, and puzzles
- How many squares - Cooperative learning worksheet with puzzle that has 40 squares. Also for team building.
- Pattern blocks
- Pattern block star challenge - Worksheet to find the angles of a trapezoid, triangle, parallelogram, and see if they can combine to make a perfect circle. Find what the Angles and Lengths of the Sides are in this pattern.
- Find the sum of four consecutive numbers, without adding four numbers.
- Squares 30 - find the squares in a worksheet
- Forty squares - find the squares in a worksheet also team building activity or cooperative learning
- Surveilence camera puzzle - Worksheet determine the best placement of cameras to surveil eight streets.
- Printable cube pattern - Worksheet
- Pythagoras theorem - Explanation sheet to justify a 2 + b 2 = c with 1. Area model & 2. lengths of sides model
- Relative position & topology - Worksheet to identify: in, on, out, for 3d & 2d pictures, & draw the 5 shapes. Age: preschool - first grade
- Tessellation - Worksheet : How to make a tessellation
- Triangles
- Triangles - properties, kinds, angles, sides, and relationships
- Medial triangle exploration & challenges - includes bisecting a line with a compass
- Triangle symbol (Check source for more)
- ▵ to make this white small triangle pointing up
enter html codes: ▵ or
▵ - to make a larger one use the code
<span style="font-size:50px;">▵</span>
You change 50 for different sizes.
▵
- ▵ to make this white small triangle pointing up
- Trapezoid 36
- Ruler and compass constructions
- Cross sections
- Square 8x8 with pattern
Tangram puzzle sets and tables



Data Analysis & Probability
Knowledge base & tools to develop mathematical literacy
Knowledge base
The mathematical knowledge base includes concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come to be literate in geometry and spatial reasoning.
- Data analysis
- Probability
- Concepts 9-12 from Science for All America s (SFAA) & National Assessment for Educational Progress (NAEP )
- Data analysis & probability vocabulary - lists of vocabulary for primary, middle, & upper levels.
- Graphing sequence -
- K - 3 average, bar graph, concrete real object graph, data, grid, picture graph, table, tally, trial. Graph the number of letters in their first name and last name and both, ages of learners in years and months,
- 4 - 6 broken line graph, descriptive statistics, equally likely events, extrapolate, frequency, generalization, histogram, inference, interpret, interpolate, line graph, line plot, mean, media, midway, mode, ordered pair, outcome, probability, quadrant, random, range, ratio, sample, scale drawin,g simple event, statistics. Graph rate of motel prices for different Monopoly places.
- 7 - 9 box plot, compound event, circle graph, error of measurement, extrapolate, mutually exclusive, outlier, quartile, scatter plot, skew, lines stem and leaf plot, whisker. What is the region bounded by y=sin(kx)+2, x=0, x=2π, and y=0, with k constant.
- Stem-and-Leaf Plotter
- Box and whisker plotter
- Statistics timeline and history
- Bias changes outcomes in a pattern. Like throwing a rock and always missing the bullseye in one direction. Noise is like throwing a rock and missing the bullseye in all directions. Noise is what makes the difference between theory and reality or the practical. Source - Noise
Information to facilitate literacy in data analysis & probability & tools to achieve it
- Probability - Development with sample problems, explanation of experimental & theoretical probability (with examples) & Reader's Theater carnival problem to solve. Teaching unit with a learning agenda to use as project based learning.
- Probability Rubric - applicable for all levels
- Probability Instructional map - Maps probability as theoretical & experimental concepts, to dice activities, & instruction with a learning cycle instructional method
- Coordinate Graphing Notes - Data sheet for data analysis, variables, relationships, and graphing
- Graph paper - 11 high 9 wide 2 cm squares
- Graph paper
- Normal curves - Visual graphs & charts with normal curve, standard deviation, z scores, stanines, percentiles, SAT, ACT, IQ, cummulative percentages, quartiles, percent in stanines
- Frequency distribution - visual examples with charts and graphs; central tendency; percentiles; and correlations
Activities to facilitate data analysis & probability literacy

Data analysis
- Bean toss for combination of addends with two dice & probability
- Find your class's hang time and vertical jump statistics - worksheet range, median, mean, mode, graph. Sample - graph paper
- One variable analysis activities - ping-pong ball race, how many stars in a minute, collect data, analyze mean, median. mode.
- Square 8x8 with pattern
Probability
Activities with spinners, dice, & coins
- Probability unit - Complete lesson plans & worksheets for 6 activities, One die & two die sum, spinners, dice, tiles in socks, coin flip, & cup flip in a unit plan for experimental & theoretical probability.
- Flippping 1, 2, 3, & 4 coins - Worksheet with hints.
- Spinners - 3 activities with spinners of equal sections, some with the same numbers and others with different numbers. Worksheet with hints and spinner patterns.
- Three coin problem - Worksheet with hints & discussion ideas
Cards
- Pick two card game - Worksheet for card game to pick two of six to win includes charts, hints, & tree diagram.
- Aces for dinner: Which version gives you the better odds? - Worksheet with hints & discussion ideas.
- Card tricks with video explantions - Magic? video to demonstrate identification by elimination or identification
- Compound probability - Plan with a stacked deck and and regular deck of cards to introduce compound probability. Includes tree diagrams.
Other materials
- BINGO
- Create your own BINGO card for 0-9 addition - Explores the probability of the number of addends for facts from 0-9, includes BINGO cards with instructional suggestions
- Creat your own BINGO card for 0-9 subtraction - Explore the probability of the number of addends for facts from 0-9, includes BINGO cards with instructional suggestions
- Sampling number of chips in a package of chocolate chip cookies - Lesson plan for a challenge activity to estimate the number of chocolate chips in a package of cookies. Also a challenge to think about & investigate the weight of a cookie before & after crumbling.
- Sickle Cell investigation - Worksheet with Background information & hints. Use of a Punnett Square to determine different probabilities theoretically & experimentally probability
- M&M® Challenge - activity directions and worksheets for data analysis, mean, median, mode, & graphing of colors of M&M's. Can be used for probability.
- Simulation to determine populations of a species and five species with capture, release, and recapture using ratio and proportion - Worksheet with hints
- Frogs in a pond problem - Worksheet as assessment of ratio, proportion, and capture release. Also used as a Thinking Puzzles: for Concrete & Formal Operational Thought Solutions
- The Case of the Carnival Probability Game - Instructional materials: Sample problem with explanation as experimental & theoretical probability & Reader's Theater script along with a carnival unit with an agenda for problem based learning.
- Body proportions - Worksheets and plan for learners to measure body parts and compare their ratios to heigh. And the use of ratio in Egyptian art, Greek sculpture and more. Learners can explore proportion of body parts and a person's height with diagrams, scatter plots, graphs, and regression lines.
- Car keys sweepstakes fair or fixed? - Worksheet with hints & discussion ideas
- Envelopes of cash or not. What are the odds? - Worksheet with hints & discussion ideas.
- Sack lunches. Teacher randomly passes out lunches. What are the odds? - Worksheet with hints & discussion ideas.
- Rubber band stretch simulation - is it proportionally accurate?
- John Snow - Analysis for a source of cholera in London, England.
- Snow's map, demonstrated the spatial clustering of cholera deaths around the Broad Street well, to provide strong evidence in support of his theory that cholera is a water-borne disease. Snow used some proto-GIS methods to buttress his argument: first he drew Thiessen polygons around the wells, defining straight-line least-distance service areas for each. A large majority of the cholera deaths fell within the Thiessen polygon surrounding the Broad Street pump, amd a large portion of the remaining deaths were on the Broad Street side of the polygon surrouding the bad-tasting Carnaby Street well. Next, using a pencil and string, Snow redrew the service area polygons to reflect shortest routes along streets to wells. An even larger proportion of the cholera deaths fell within the shortest-travel-distance area around the Broad Street pump. Picture book with maps for younger grades is Evidence by Deborah Hopkinson, 2024. 40 pgs.
- Finding Pi with probability . Use a toothpick, nail, or needle & sheet of construction paper. Draw parallel lines that are spaced apart the length of the nail across the width of the paper for the length of the paper. Drop the needle from about a half meter above the paper and record if the toothpick lands on a line or not 50 times. Calculate the ratio and see how close it is to π (pi = 3.141592653589793...)
Ratio and Proportion information

Measurement
Knowledge base & tools to develop mathematical literacy
Knowledge base
The mathematical knowledge base includes concepts necessary for learners to conceptualize to become mathemtically literate and misconceptions that must be over come. Includes Measurement & estimation concepts & misconceptions.
Information to facilitate literacy in measurement & tools to achieve it (pedagogy)
- Development of measurement is dependent on
- Child and adolescent development, the ability to
- Conserve and perform conservation tasks,
- Unitizing, visualization of units of measurement, and conceptualization of the
- Knowledge base measurement concepts and relationships between different measures.
- Cartography unit - measuring with map making, angle measurement, compass, clinometer, measure height, measure distance, locating objects with distance and angle combinations, contour maps
- Calendars 1776 - 2000 - Printable page. Can you discover the day of the week, day that different people were born? Perpetual calendar for 1776 - 2000
- A History of Measurement in the United States - Timeline
- History of the metric system in the United States - Essay
- Measurement unit - Includes lesson plan, activities, & worksheets for linear, volume, mass, & density. for middle level learners. Aksi includes.
- Link to SNL metric and Washington's speech.
- Metric fact sheets - Types of metric units, their prefixes, & values - meter, liter, & gram, Prefixes on a number line, Modle diagram of dust particle & human hair, Metric prefixes, symbols & exponential powers to + & - powers of thirty.
- Metric review / quiz - Worksheet & word bank with answers
- Crossword puzzle - metric system review
- Outcomes by levels - Developmental list of linear, area, volume, capacity, weight, mass, time, money, temperature, estimation outcomes
- Telling time activities - Procedures and activities to teach time at second grade Includes sample pictures
- Timelines : American Education: people, events, and ideas that shaped American Education, Significant Historical Political Events in Human, Development of Significant Science, Mathematical, & Technological Events, History of media and children' literature, & Statistics timeline and history.
- Measurement vocabulary - lists of vocabulary for primary, middle, & upper levels. Also includes:
- Measurement outcomes - linear, area, volume, capacity, weight, mass, time, money, temperature, estimation. by levels
Historical weights found around the world suggest traders recognized the need for standard measurements.

Activities to facilitate measurement literacy
-
 Introductory activities should have learners directly compare objects as big and little. Compare hands, clothes, bowls, eating utensils, toys, crayons, blocks, and more. Then have them directly compare and order three objects as big, medium, & small. Work towards sequencing larger sets of objects.
Introductory activities should have learners directly compare objects as big and little. Compare hands, clothes, bowls, eating utensils, toys, crayons, blocks, and more. Then have them directly compare and order three objects as big, medium, & small. Work towards sequencing larger sets of objects. - Use non standard units to measure all sorts of objects.
- Measurement unit - primary level introduction to measurement with first straw activity to develop a concept of standard units of linear measurement , then similar hands on measurement activities for volume, mass, & temperature.
- Measuremen unit - middle level review of linear, mass, volume, measurement of matter, with an introduction to density with directed inquiry activities & blank learner lab notes
- Metric fact sheets - Types of metric units, their prefixes, & values - meter, liter, & gram, Prefixes on a number line, Modle diagram of dust particle & human hair, Metric prefixes, symbols & exponential powers to + & - powers of thirty.
- Observation & measurement unit - How do we observe? properties to observe, change, measurement, properties to measure, & measurement procedure worksheet
- Density unit - learning cycle inquiry activities for middle grade to apply measurement: linear, mass, volume, of matter to calculate density of solids, liquids, & gases. Includes 14 activities with lesson plans & lab sheets.
- Cartography map making, angle measurement, compass, clinometer, measure height, measure distance, locating objects with distance & angle combinations, contour maps,
- Measuring heights of trees & other objects - clinometer, shadows, scale (Biltmore) stick
- 21 Centimeter card game : make a deck with 45 cards. Draw a slanted straight line (at different degrees on each card) with the following lengths, on cards as listed below:
- 4 cards each with a - 1 cm line,
- 4 cards each with a - 2 cm line,
- 4 cards each with a - 3 cm line,
- 4 cards each with a - 4 cm line,
- 4 cards each with a - 5 cm line,
- 5 cards each with a - 6 cm line,
- 5 cards each with a - 7cm line,
- 5 cards each with a - 8 cm line,
- 5 cards each with a - 9 cm line, &
- 5 cards each with a - 10cm line.
- Linear & volume -
- Solar system - big distances & volume activities (5E learning cycle) to explore the size and relative position of the solar system aligned to the Common Core Standards, Next Generation Science Standards, National Science Education Standards, & 21st Century Skills: critical thinking, communications and measurement.
- Temperature How does temperature in centigrade Celsius compare to temperature in Fahrenheit? Facts: Water freezes at 32 degrees Fahrenheit and 0 degrees Celsius. Water boils at 212 degrees Fahrenheit and 100 degrees Celsius. Find a thermometer that has both scales and read from one scale to the other. C = (F - 32) * 5/9; C = (F - 32) / 9/5; F = (C * 9/5) + 32 Verify or prove the formulas.
- Money - Sequence of outcomes to develop with activities to learn to count change:
- Know people use money to buy goods and services.
- Sort money by its appearance.
- Draw pictures of coins and paper money.
- Select coins on their desk (penny, quarters, dimes and nickel) as called.
- Identify and state the values of money (penny = 1 cent , quarter = 25 cents, dime = 10 cents, nickel = 5 cents, ... ).
- Sort money by its value.
- Order money by its value.
- Recognize different coins can have similar values.
- Represent coins and their values: draw a circle for each coin (penny, quarter, dime, nickel) with the value inside: (25, 25, 10, 10, 5).
- Identify a coin, its value, and point to its value represented on a number dot sequence, trail, or line . Select a second coin. Identify the coin, its value, and show how to add and represent its value and sum of both.
- Identify a coin, its value, and point to its value represented on a labeled hundreds chart . Select a second coin. Identify the coin, its value, and show how to add and represent its value and sum of both. Draw an arrow from 1 to the value of the first coin. Circle the value and draw an arrow for the value of the next coin and circle the sum. (arrow math)
- Use arrow math and a labeled hundreds chart chart to solve coin problems with two addends.
- Use arrow math and a labeled hundreds chart chart to solve coin problems with more than two addends.
- Given an assorted collection of coins (that add to less than 100 cents), Use arrow math and a labeled hundreds chart chart to solve coin problems with more than two addends.
- Identify different orders to count change more efficiently. (Start with the largest coins, group similar coins, group by easy numbers (10, 50, 100, & 25).
- Repeat the above procedures on a blank hundreds chart .
- Repeat the above procedures with paper money.
Game play : Deal three cards to each player and play like 21. Player that line lengths add closest to 21 cm, without going over is the winner. After the deal each player can choose to be dealt another card or hold. Player closest to 21 cm, with out going over wins. Winner measures each card with a cm ruler to verify their score.
Alternative version : Play as above and record the lengths of their cards, if they don't go over 21. First player to 121 wins.
Can use the counting money strategy for counting decimal numbers. Write the starting value (1.89), select a count (.01), write it, write the sum (1.90), write the next coin (.10), then the sum (2.00), and continue as before.

Process dimensions of mathematics
Information to plan and facilitate the learning and use of skills in the process dimensions of mathematics.
Problem solving Tools to facilitate mathematical problem solving
- Problem solving oncepts, misconceptions, & outcomes by levels in the mathematical knowledge base
Information to facilitate literacy in problem solving & tools to achieve it
- Development of problem solving - page contents includes:
- Heuristic :
- Strategies for solving problems with sample problems
- Planning & teaching tools pedagogical and curriculum
- Teacher's role in problem solving
- Suggestions to help learners solve problems
- Assessment sample questions to assess learners' mathematical problem solving
- Characteristics of a good problem ideas to consider when writing or selecting problems
- Planning questions to prepare to facilitate problem solving & investigating suggestions to consider when writing or planning to use problems
- Problem Solving Goals and Outcomes to review for the inclusion in appropriate curricular documents and plans
- Problem solving vocabulary to introduce to learners
- Dispositions to review & select to focus on
- Learner's materials
- Learners problem solving guide or checklist to use to as a guide with suggestions to solve problems
- Learners solving checklist - with before, during, and after suggestions
- Learners Solving Attitude Inventory with yes - no questions
- See also communication dimension -
Activities to facilitate problem solving
- Assorted problems
- Bucket problems application of addition, subtraction, problem solving, combinations, reasoning.
- How many squares? Problem / activity
- Teaching notes for forty squares problem / activity
- Problems to solve by strategy for solving
- Expressions & formulas - Bus, train boarding and deboarding problems for problem solving, expressions & recursive formulas, problem solving strategies of working backwards& acting out
- Sack Lunches - Teacher randomly passes out lunches. What are the odds? - Worksheet with hints & discussion ideas.
- Acrobats Logic Problem - Worksheet draw a diagram, proportion & problem solving diagrams
- Sack Lunches- Teacher randomly passes out lunches. What are the odds? - Worksheet with hints & discussion ideas.
- Wages for Pet Care
- Acrobats Logic Problem - Worksheet draw a diagram, proportion & problem solving diagrams
- Mysteries as problems - Making word problems interesting. I used Which witch is which on Halloween and students really enjoyed solving the problems iin that mystery ...
- Magic triangle
- Magic square perimeter
- Mazes - 4 traditional student made mazes and a number maze to use as an outdoor jumping activity. Working backwards or both ways problem solving strategy
- Cartesian coordinate four in a row game - lesson plan & linked worksheet
- Polar coordinate four in a row game - lesson plan & linked worksheet
- Skyline and buildings puzzles - solve the placement of buildings in a 3x3 grid and 4x4 grid. Sudoku like that uses perspective for a relative position to create & solve problems.
Reasoning and proof
- Reasoning & proof Concepts, misconceptions, & outcomes by levels in the mathematical knowledge base
Information to facilitate literacy in reasoning & proof & tools to achieve it
- Reasoning and Proof Explanations and development of reasoning, proof, & logic - information on reasoning and proof with examples of different types of proof, teaching suggestions, & an extensive scoring guide
- Reasoning and proof big idea, concept, or generalization instructional planning map
- Development of reasoning from birth to maturity
- Reasoning, conservation, and cognitive development tasks & activities
- Application of proof by elimination & verification with a card trick
- Bucket problems reasoning, proof, conjecture, combinations
- Decision making, critical thinging, and change processes
- Structure for Analyzing and Presenting Arguments
- Logical Reasoning and Reasoning Errors
- Position analysis
- Issue analysis & sample issues analysed for democratic education for all
- Reasoning solutions for SUDOKU - introduction to teminology, with an example puzzle with solution, list of solution methods, free puzzle source, & solution generator
- Imagining
- An Outline of Goals for a Critical Thinking Curriculum and Its Assessment
- Magic triangle
- Magic square perimeter
Activities to facilitate reasoning & proof
- Bucket problems application of addition, subtraction, problem solving, combinations, reasoning.
- How many squares? Problem / activity
- Teaching notes for forty squares problem / activity
- SUDOKU
- Jo Tall and Jo Short - Worksheet ratio & proportion activity, historical research problem used to investigate the develop of reasoning as suggessted by Piaget
- Acrobats Logic Problem - Worksheet draw a diagram, proportion & problem solving diagrams
Representation
Representation Concepts, misconceptions, & outcomes by levels in the mathematical knowledge base
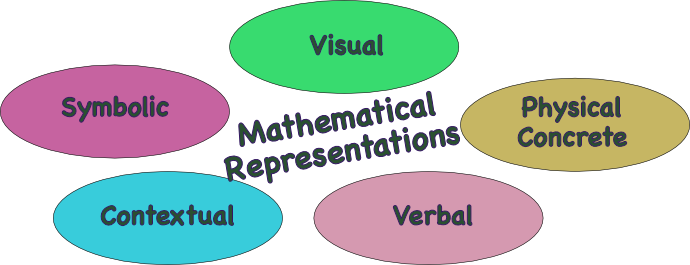
Information to facilitate representation & tools to achieve it
- Examples of mathematical representations with language as nouns and verbs.
- Function exploration - includes definitions with examples, diagrams, & representations including a function machine. Also activity with worksheet and charts to explore a function with a variable factor (3) & constant factor (27) & discover casting out nines
Area representations
Lynne Outhred and Michael Mitchelmore asked learners to illustrate the area of a rectangular shape. They found learners demonstrated four different strategies: incomplete covering, visual covering, concrete covering, and measurement. The drawings below show samples from each.

Representation of relative position of objects
Illustration of Internal Representation

Actual object, real world, or external representation
Representation of external objects with points on an other external object

What does this have to do with mathematical representations?
Activities to facilitate representation
- Representations of 21 / 7 or π.
- Area & perimeter - pools and sidewalks - Worksheet patterns, relationships, & functions with area and perimeter
- Growing squares challenge - - Growing square swith toothpics challenge. Includes picures or slides that step through adding toothpicks to grow squares, record data in a table, to show the pattern of increasing squares and increasing toothpicks.
- Growing squares worksheet - Use toothpicks to find a pattern & formulas to determine the number of toothpicks added to make larger squares. Toothpicks in the perimeter, toothpicks to make the squares in the squares, and the number of squares in the growing squares.
- Toothpicks in a rectangular pattern - Worksheet with hints to write equations for the sums of toothpick patterns in a rectangle and discussion ideas for what is an equation, function, and can they be both.
- Pattern activities - Investigatons to develop patterns & formulas. Starting with number strips, dot patterns & other growing patterns: v, w, pyramid, prism, tower, triangle, rectangle, log stack, can stack, hand shake, dancers, step pyramid, & disc ...
Communication
Communication Concepts, misconceptions, & outcomes by levels in the mathematical knowledge base
Information to facilitate literacy in communitation & tools to achieve it
- Different ways to communicate problems with sample problems
- Ways to communicate mathematical representations as objects, properties, actions, & operations
- Graphing with line graphs as communication
- Graph paper
Activities to facilitate communication
Connections & perspective
Connections & perspective Concepts, misconceptions, & outcomes by levels in the mathematical knowledge base
Information to facilitate literacy in connections & perspective & tools to achieve it
- Mathematical ideas build upon each other.
- Mathematical ideas are connected to other mathematical ideas.
- Mathematical ideas are connected to the world.
Activities to facilitate reasoning & proof
Technology, computer programming, software, 3D printing
--- Coding software ---
Mozilla free
Google free
- Made with code - projects, mentors, resources ...
Technology
- History of the cell phone Read ... Cell phone mathematics . The story of how Brad Parkinson used creativity and mathematics to enable the use of cell phones.
Math software
- History of graphing software Read : The Graphing Calculator Story by Ron Avitzur, then below the article are links to download the software.
Coding resources
- Spies in the Computer - basic software program and class activity on a 10 x 10 grid
Pedagogical resources
- Viewpoint: Arguments for a LOGO - Pascal Computer Curriculum
- Logo dissertation review by Barbara Elias - Dealing with Logo and the transfer of knowledge from learning one programming program to learning another
3 D printing
*********************
Last edited - February 25, 2026
Quick links to math topics:
- Mathematical knowledge base of concepts & outcomes
- Pedagogical knowledge to develop professionally and to create learning experiences to facilitate mathematical literacy with teacher tools to assist.
- Problems & activities listed by their dimensions.
- Pedagogy information
- Activities - Units, activities & problems to development mathematical ideas, by dimensions:
Content : dimensions
- Number value & Operations (addition, subtraction, multiplication, & division)
- Activities - problems, units, packets ...
- Algebra, Patterns, Ratio, & Proportion
- Activities - problems, units, packets ...
- Geometry & Visual spatial reasoning & representation
- Activities - problems, units, packets ...
- Data Analysis & Probability
- Activities - problems, units, packets ...
- Measurement
- Activities - problems, units, packets ...
Process dimensions:
- Technology - calculator, programming, & other math related tech ideas
*********************

*********************
There are 10 kinds of people in the world. Those who understand binary and those who don't.
*********************
Jeffery Weld asks:
Why is it whenever students don't do well on a national test the news agencies report one or a few particular items that were on the test by stating the test questions, then they believe it is necessary to provide the answers.
*********************
If their listeners need the answers, why should we expect students to be able to answer it correctly?
*********************
The Jibaro Indians of the Amazon rain forest express the number five by the phrase:
"wehe amukei,"
"I have finished one hand,"
and the number ten by
"mai wehe amukei,"
"I have finished both hands."
*********************
"These landmarks must not be treated as objectives to be marked off. The goal is to mathematize not pass landmarks. Enjoy the journey create systems to do mathematics with the knowledge that students have. One should recognize the fallacy of thinking there can be one activity or sequence of activities for all students."
*********************
One of the universal customs that man has successfully established on earth is the
Hindu - Arabic numerals
to record numbers.
*********************
Math is meditation for thinking about the world.
*********************
Geometry is the science of correct reasoning on incorrect figures.
*********************
Galileo was put under house arrest and allowed visitors, but no mathematicians .
*********************
Common sense & knowledge
*********************
Counting in Winnebago:
- WI n
- NO n BA
- THABTHI n
- DUBA
- SATO n
- SHAPE
- PETHO n BA
- PETHABTHI n
- SHO n KA
- GTHEBO n
*********************
Interesting book:

The Power of Logical Thinking: Easy Lessons in the Art of Reasoning... and Hard Facts About Its Absence in Our Lives, Marilyn Vos Savant (1996) ISBN 0-312-13985-3 Saint Martin's Press: New York.
*********************
Olber's Paradox
If the universe is infinite in time and space, stars should occupy every point in space and fill the night sky with light.
*********************
*********************
*********************
*********************
Directory links:
*********************
Mathmaticians think about more than math.
Earth will run out of the basic resources, and we cannot predict what will happen after that. We will run out of water, air, soil, rare metals, not to mention oil. Everything will essentially come to an end within fifty years. What will happen after that? I am scared. It may be okay if we find solutions, but if we don’t, then everything may come to an end very quickly. Mathematics may help to solve the problem, but if we are not successful, there will not be any mathematics left, I am afraid!
*********************
U.S. Students
Score in the top tier on
the PISA 2012 Math Creative Problem SolvingAssessment
*********************

*********************
*********************
*********************
Measurement is never exact.
It is only as accurate as who and with what is doing the measurement.
*********************

*********************

*********************
*********************

*********************
Read ...
The story of how Brad Parkinson used creativity & mathematics to enable the use of cell phones.
*********************
Data is just numbers. They need an explanation or theory to make it data.
*********************
Algebra was greatly advanced by al-Khwarizmi’s book:
Hisab al-jabr w'al-muqabala From which the word algebra came.
*********************
Long standing math concerns -
Still pertain ...
Most students are funneled into a single pathway (or track), even though career aspirations differ.
Almost all student in the US are required to study mathematics yearly through at least 10th grade. Distinctive to the US is that, independent of their intended Major [roughly 60% of secondary students do not intend to major in STEM].
Secondary students who plan to attend college typically take mathematics courses from the calculus track through 11th or 12th grade, the latter if they plan to attend selective institutions or major in STEM.
1. Failure and retake rates in high-school mathematics classes have been consistently high, sometimes as high as 50% per year, for decades.
2. Students from underrepresented ethnic and socioeconomic groups experience considerably higher attrition rates. These students are disproportionately filtered out of mathematics and science. Racial performance gaps in mathematics have remained intractable for decades. This is a major societal issue, the causes of which include differential access to resources such as up-to-date curricula, qualified teachers, and current technologies, as well as placement systems that assign students of color disproportionately to "remedial" tracks. In addition, however, specific mathematics courses, beginning with algebra, are major factors in failure and dropout rates.
3. Historically, course sequences that deviated from the calculus track tended to lead nowhere, creating the perception that any new proposed pathway will lead nowhere.
Decades ago, for example, shop math and business math allowed students to meet mathematics requirements for graduation but did not provide skills that would enhance their employability or enable them to proceed academically beyond high school. Recent discussions about courses in data science have hinged on questions of whether those courses will adequately prepare students for calculus or for college admission. As increasing numbers of students intend to enroll in college, the path to calculus continues to be seen as the preferred route, despite arguments for the growing importance of data and statistical reasoning.
Source
"More math, less “math war”
by Alan Schoenfeld and Phil Daro Science March 22, 2024.
Also check out:
Beyond the Math Wars:: Focus on teachers to improve instruction. By Rachel S. McClam, Rebecca A. Cruz. Dec 2, 2024
*********************



