Patterns
Pattern exploration and investigation activities
Do not follow where the path leads. Rather, go where there is no path and leave a trail.
Ralph Wald Emerson
Page Overview:
- Overview
- Concepts & outcomes
- Math & science content concepts & outcomes
- Problem solving & inquiry concepts & outcomes
- Pedagogical ideas
- Activities
- Number strips - even, odd, multiple of three
- Hint box
- Dot patterns - even, odd, & adding strips & patterns
- V & W patterns -
- More dot patterns - band & director model, name this model,
- Data tables and patterns -
- Adding patterns with number strips
- Arithmetic Sequences with tables and strips
- More arithmetic sequences - use an expression and make a table, strip, or dot pattern
- Pyramid sequences
- Prism sequences
- Tower sequences
- Triangular numbers
- Rectangular numbers
- Log stacks
- Can stacks
- Handshake problem
- Dancers problem
- Step pyramid problem
- Disc problems
- Truss problems
- Brick patterns
- Staircases - rise & run pattern
- S Pattern
- Blank graph sheet
Overview
Patterns are recognized by very young learners. They are interesting and used by children when they are playing. Constructing two dimensional shapes with paper, drawing on paper, tiles, pattern blocks;and three dimensional shapes with blocks, clay, folding paper and so forth.
A first pattern, lining blocks or objects up in a line or train can be represented as counting: 1, 2, 3, 4, 5, … Later rectangular stacks of blocks, pyramids of blocks, different drawing different shapes from a basic shape and other visually pleasing designs.
Patterns which can be represented numerically as:
- 1, 2, 3, 4,
- 0, 2, 4, 6,
- 1, 4, 9, 16,
- 1, 7, 19, 31,
This page includes information to plan and use activities for patterns. It includes concepts in mathematics for: patterns, algebra, representation, tables, charts, graphs, geometry, problem solving, reasoning, visual representation,
Pattern is a repeated design, sequence, structure, change of properties, shape, position, or changing of quantity.
Concepts and outcomes
Mathematical
Concepts
- Patterns can be represented with words, pictures, symbols, numbers, tables, diagrams, charts, graphs, equations, formulas, models, simulations, animations, videos
- Patterns described with recursive and direct formula.
- Different ways to communicate and represent patterns have different advantages.
- Appreciate an elegent representation and formula.
- Recursive formula uses a current measurement and adds to it a constant: next shape = current + constant.
- Direct formula is a formula that uses a constant amount and multiplies it by the pattern number: next shape = current shape + (constant * pattern number).
- Formula is an equation that states a rule about a pattern.
- Recursion uses a current value to find the next value.
- Sequence is an order in which numbers or things follow each other.
Mathematical concepts, misconception, and outcome knowledge base
- Data analysis
- Patterns & algebra
- Patterns
Outcomes
- Describe patterns with dots, on number strips, tables, and other visual and non visual representations.
- Use recursive formulas to describe number sequences.
- Use expressions and direct formulas to describe number sequences.
Problem solving & inquiry concepts and outcomes
Pedagogical ideas
Activities sequence
- Number strips - even, odd, multiple of three
- Hint box
- Dot patterns - even, odd, & adding strips & patterns
- V & W patterns -
- More dot patterns - band & director model, name this model,
- Data tables and patterns -
- Adding patterns with number strips
- Arithmetic Sequences with tables and strips
- More arithmetic sequences - use an expression and make a table, strip, or dot pattern
- Pyramid sequences
- Prism sequences
- Tower sequences
- Expansion ideas
Focus questions
- What is a pattern?
- What objects, events, or systems can make a pattern?
- What are different types of patterns?
- What properties indicate patterns?
- Identify different ways to create patterns?
- Do patterns change in the same way?
- Do patterns alway change in a constant way?
Related resources
Expansion resources
- Stairways and box stacking problems
- Growing squares & area perimeter activities
- Pools & sidewalks problem or growing squares - An eccentric person wants to make containers, or pools, with sidewalks around them. The only requirement is the pool and sidewalk sections have to be square...
- Toothpicks - Growing squares challenge worksheet. Use toothpicks to find formulas to determine the number of toothpicks added to make larger squares. Toothpicks in the perimeter, toothpicks to make the squares in the squares, and the number of squares in the growing squares.
- Toothpicks - Growing squares challenge slides for the challenge above. Slides step through adding toothpicks to make growing squares, record data in a table, and ind the a pattern of increasing squares and increasing number of toothpicks.
- Body Proportions, height, body parts, bones, & Egyptian art
- Multiplication of whole numbers, multiplication of binomials (x+1)(x+1), & area patterns
- 8x8 Square patterns with three colors -visual geometric pattern
Activities
Number strips
Notice the alternating colors on the number strip. They start with zero and the other end is torn. 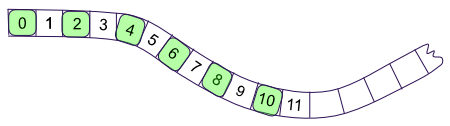
- What do the two ends of the strip represent?
- What do the different colored numbers have in common?
- Think of a number not on the strip. What color would it be if it were on the strip?
- What is a rule for the green numbers?
- What is a rule for the other numbers?
- How do you know what color a number like 222, 549 is?
Use the table to summarize the patterns.
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | Pattern rule |
|---|---|---|---|---|---|---|---|
| Green pattern | |||||||
| Red pattern |
Here is another number strip.
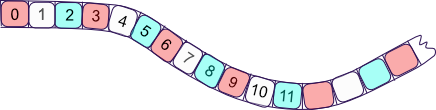
- What do the different colored numbers have in common?
- Think of a number not on the strip. What color would it be if it were on the strip?
- What is a rule for the red numbers?
- What is a rule for the blue numbers?
- What is a rule for the light numbers?
Use the table to summarize the patterns.
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | Pattern rule |
|---|---|---|---|---|---|---|---|
| Red pattern | |||||||
| Light pattern | |||||||
| Blue pattern |
Hint box:
n is for the pattern number
- n + 1
- 2n
- 3n
- 2n + 1
- n + (n = 1)
- 4n + 1
- 2(2n + 1) - 1
- 11 + 5n
- 13 + 4n
- 24 + 9n
Recursive formula or Step by step formula describes a sequence by building from a current number to the next. Like: next number is found by using the current number and changing it by a constant number or procedure.
- Start number = 0
- Next number = Current number + constant
A direct formula describes a sequence with a sequence number (n). N = 2n for even numbers if Start number = 0; N = 2n + 1 for odd numbers if Start number = 0; N = 3n for multiples of three if Start number = 0
Euler's formula; Vertices - Edges + Faces = 2
- V = n + 1; V= 2n; V = 2n + 1
- E = 2n; E = 3n; E = 4n
- F = n + 1; F = n + 2; F = 2n + 1
Dancers:
One flips over 5 with assists from 2, 3, 8, 9; 7 dance maneuver with 4; & 10 with 6.

R = 3L + (L-1) [there are others]
Dot patterns
Patterns can be made or represented with dots.
What does the pattern represent?
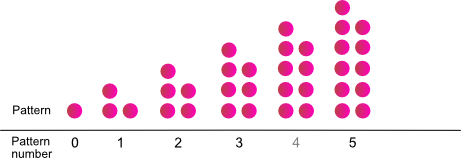
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots for a pattern number | ||||||
| Change of the dots from previous pattern |
- What is the pattern for how dots are added?
- What would be an expression to explain how many dots are in a pattern number?
- What numbers on the green red number strip do the dots represent.
Here is another dot pattern.
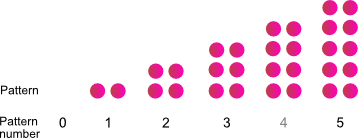
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots | ||||||
| Change |
- What is the pattern?
- What would be an expression to explain how many dots are in a pattern number?
- What numbers on the green red number strip do the dots represent.
Dot patterns and number strips together
Use ideas from both dots and number strips to think about patterns.
One of the dot patterns represents odd numbers and the other even numbers.
What color on the number strip represents odd?
What color represents even?

When you add even numbers, what kind of number do you get?
When you add odd numbers, what kind of number do you get?
If you visualize even numbers as dots, what happens when two are put together?
If you visualize odd numbers as dots, what happens when two are put together?
What if you add an odd and even number, what do you get?
Write three statements for adding odd and even numbers.
1.
2.
3.
Dot patterns with the red, light, and blue number strip.

Draw a pattern of dots for Red numbers in the pattern.
Draw a pattern of dots for Light numbers in the pattern.
Draw a pattern of dots for Blue numbers in the pattern.
Write a recursive formula and a direct formula for each colored pattern.
Recursive formulas
- Red
- Light
- Blue
Direct formulas
- Red
- Light
- Blue
What happens when different colored numbers are added? (R + L = ?) What color do you get?
Use the table to record the colors of the sums.
| + | R | L | B |
|---|---|---|---|
| R | |||
| L | |||
| B |
V and W patterns
Write the formulas for each
V pattern
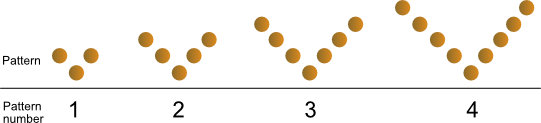
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots |
Recursive formula
Direct formula
W pattern

Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots |
Recursive formula
Direct formula
Dot patterns
Band and director pattern
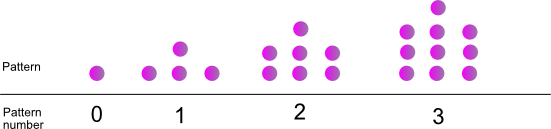
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots |
Recursive formula
Direct formula
Name this pattern
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Dots |
Recursive formula
Direct formula
Data tables
Theater in the half round
A theater has four sections that start with four seats in the first row and add seats as the seating moves from the stage to the back of the theater. The seat pattern is started in the table.
Pattern number |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Seats per section per row | 5 | 5 | 5 | 6 | 6 | 6 | 7 | 7 | 7 | 8 | 8 |
How many seats if there are 36 rows in the theater?
More data table problems
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| 25 | 41 | 65 |
Enter the missing numbers in the table.
Write a recursive formula.
Write an expression for the pattern.
Write a problem to fit the pattern.
I start with 25 ________ and ...
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Seats per section per row | 50 | 48 | 46 |
Enter the missing numbers in the table.
Write a recursive formula.
Write an expression for the pattern.
I start with 50 ________ and ...
Adding Patterns with number strips
What pattern will there be an odd and even number strip are added?
What numbers will be on the new strip?
Make an even number strip (0, 2, 4, ...)

Make an odd number strip (1, 3, 5, ...)

Add the numbers on the even and odd number strips to make a third number strip (1, 5, 9 ...)

The pattern can be made with dots.
Write an expression for it.
How do the expressions for even and odd compare to it? (2n; 2n + 1; 4n + 1)
Use dot patterns and show how the dots can be rearranged from two patters in a pattern to make a third pattern.
Arithmetic sequences
The data in the tables make arithmetic sequences.
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Sequence A | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | 51 |
Use the data to make a number strip.

Number strip A
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Sequence B | 13 | 17 | 21 | 25 | 29 | 33 | 41 | 45 | 49 |
Use the data to make a number strip.

Number strip B
Put numbers on number strip C so that strip C = strip A + strip B.
Number strip C

Write expressions.
Number strip A
Number strip B
Number strip C
Write a paragraph describing the relationship of arithmetic sequences A, B & C.
More arithmetic sequences
Make a table, number strip, and dot pattern for the expressions.
Sequence D ; 9 + 3n
Sequence E ; 4 + 5n
Write your own
Sequence F ;
Pattern number |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Sequence |

Sequence
Pyramids
Three dimensional figures have three common properties:
- Vertices
- Edges
- Faces
Use the prism diagrams, record the numbers of these properties in the table below, and find formulas for them and the relationships among them.

Pyramid |
1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| Vertices | ||||||
| Edges | ||||||
| Faces |
Write a formula for the sequence increase of vertices.
Write a formula for the sequence increase of edges.
Write a formula for the sequence increase of faces.
Euler's formula; Vertices - Edges + Faces = 2 describes the relationship between the vertices, edges, and faces.
Explain how the formula fits with the pyramid sequences.
Show how the formulas for pyramids relate to Euler's formula.
Prisms
Three dimensional figures have three common properties:
- Vertices
- Edges
- Faces
Use the prism diagrams, record the numbers of these properties in the table below, and find formulas for them and the relationships among them.
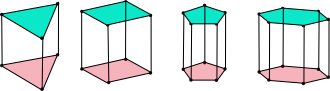
Prism |
1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| Vertices | ||||||
| Edges | ||||||
| Faces |
Write a formula for the sequence increase of vertices.
Write a formula for the sequence increase of edges.
Write a formula for the sequence increase of faces.
Euler's formula; Vertices - Edges + Faces = 2 describes the relationship between the vertices, edges, and faces.
Explain how the formula fits with the prim sequences.
Show how the formulas for prisms relate to Euler's formula.
Towers
Three dimensional figures have three common properties:
- Vertices
- Edges
- Faces
Use the prism diagrams, record the numbers of these properties in the table below, and find formulas for them and the relationships among them.
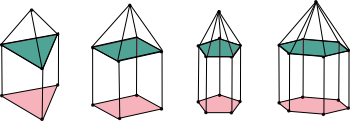
Tower |
1 | 2 | 3 | 4 | ||
|---|---|---|---|---|---|---|
| Vertices | ||||||
| Edges | ||||||
| Faces |
Write a formula for the sequence increase of vertices.
Write a formula for the sequence increase of edges.
Write a formula for the sequence increase of faces.
Euler's formula; Vertices - Edges + Faces = 2 describes the relationship between the vertices, edges, and faces.
Explain how the formula fits with the tower sequences.
Show how the formulas for towers relate to Euler's formula.
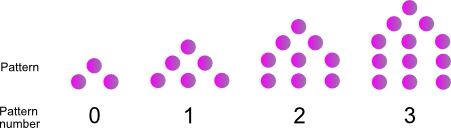
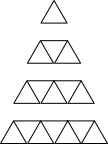
Triangular numbers
Here is a dot pattern and triangle shapes pattern. Make a table, find the pattern, write an expression
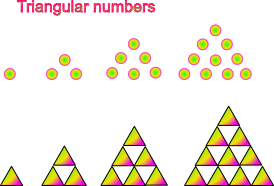
Pattern number |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
Rectangular numbers
Look at the different rectangular numbers and find a pattern to determine the number of rectangles in a pattern.
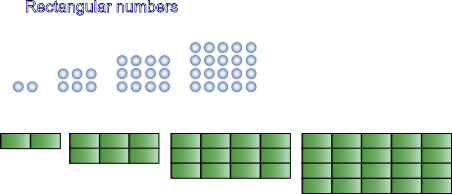
Write your formula, create some problems and describe them with representations.
Log stacks
Write an expression to determine the number of logs in a stack or the number of logs in different rows of a stack.
Then make some log piles and use the expression to answer different problems.

Can stacks
Write an expression to determine the number of cans in a stack or the number of cans in different rows of a stack.
Then make some stacks of cans and use the expression to answer different problems.
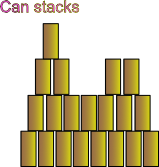
Draw your stack, write your problem, and share it.
Hand shakes problem
Write the number of students in your class or other group.
If you were to talk to each person or shake their hand, how many talks would you have or how many hand shakes would you make?
The diagram below represents students, hand shakes, or talks.
Find a pattern and use it to answer some questions.
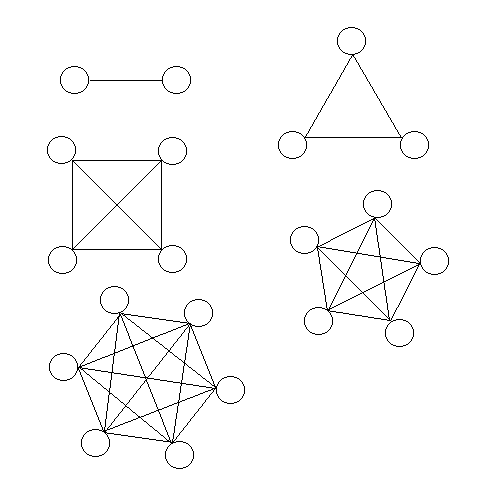
Number of students.
Number of shakes or talks.
How many shakes for _____ students?
How many students would there need to be to shake 200 different hands?
How does the total talk time increase if you talk to each person for 2 minutes?, 4 minutes, 6 minutes, ... 15 minutes?
Dancers problem
A dance choreographer wants ten dancers to start in the triangle pattern labeled start and have the least number of dancers move from their position to invert the triangle, as in the triangle labeled finish.
What is the least number of dancers that would have to move from their start positions to invert the triangle?


Describe a solution in three position changes.
Hints:
It might be helpful to number the dancers so when you talk to others, you will know which dancers are moving positions and which are not.

Find a pattern for these triangular shapes (next 15 dancers). Then find a pattern for how the number of dancers would need to move to invert the triangle.
Step pyramid problem
The diagram below shows a plan present to a pharoah to build a step pyramid.
If the center block is used as a cubic unit, how many blocks or cubes are needed to build it?
Step pyramid plan

Let's say that after the pharoah sees the pyramid, she thinks it needs to be higher. Of course the construct team needs to know how many more blocks will be needed. Find the pattern for the number of blocks needed to continue the pattern one cube higher, two cubes higher, and so on.
Disks problem
A company makes and sells metal discs. Some of which have holes punched in them. The holes are to make the discs lighter and they are punched in a way to make them balanced. Here are two discs.
What is the pattern?

How man holes would the next discs have?
Using this pattern, what would be the number of holes in the first disc that with more than 100 holes?
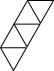
Trusses
Truss is a framework used to support a floor, bridge, roof, and other structures. They are often constructed with metal and lumber with triangular shapes.
Equilateral triangles can be used to make trusses. What is the pattern for adding triangles as trusses increase in size?
Truss sizes: 1, 2, 3, 4
Draw the truss, enter the length of the beam and the number of rods.
Truss |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Length of beam | 1 | 2 | 3 | 4 | |||||
| Number of rods |
Describe the pattern.
Write a recursive formula.
How many rods are needed for a beam of ______ length?
Find a formula to find the number of rods (R) for a beam of any length (L).
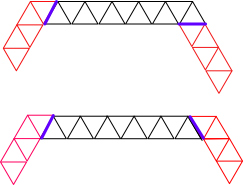
Consider two truss lengths.
Six long
![]()
Three long
If we consider joining these two trusses at their sides, there are two places they can be joined.
![]()
Consider all the ways a six and three truss can be joined.
Combinations for joining six and three length trusses.
An outdoor shelter company makes shelters with two foot rods. They join three trusses, which they mount on two pilars.
Complete the table so it lists the sizes of the production trusses (short & long), their lengths, the length of the finished three part truss, and the rods used to make each.
|
Rods | Length |
|---|---|---|
| Short truss | ||
| Long truss | ||
| Joined truss |
The company will usually use three length trusses (6 foot) for the sides, but the length of the roof may vary from five truss lengths (10 foot) to ten truss lengths. Make a table for the number of rods needed for each truss.

|
Side | Roof | Total |
|---|---|---|---|
| Five | |||
| Six | |||
| Seven | |||
Creat a problem of your own and share it.
Brick patterns
Bricks are three dimensional and the diagram below shows the size of a standard brick.

Below are four repeating brick patterns for a starting course.

This is not a repeating brick pattern.
![]()
How many bricks are needed to make each pattern?
Course |
Pattern | Number of bricks to make a pattern |
|---|---|---|
| Course A | L ... | |
| Course B | S, L, | |
| Course C | ||
| Course D |
A mason wants to know a formula to calculate the number of whole bricks and half bricks needed if they know the number of patterns.
Course |
Formula |
|---|---|
| Course A | Total bricks = Number of patterns * number of L bricks T = (N*L) |
| Course B | |
| Course C | |
| Course D |
The number of bricks needed for a particular wall will depend on: the length of the wall, how the pattern ends, if the pattern is to be symmetric, and the size of the mortar joints.
A client has a ten foot wall inside an entry way that they want to brick with a pattern. The wall is eight foot tall. Design a pattern and calculate the number of bricks needed.
Creat a problem of your own and share it.
Staircases

Construction of stairs is an interesting process, which depends on two important values, known as the run and the rise.
Too investigate some stair patterns let's start by making a stair model.
Print the diagram below and make a staircase model.
Directions:
- Cut a slit along the line from A to C.
- Cut a slit along the line from B to D.
- Make nine accordion folds with the lines DC to AB.
- Square the stairs and fold where the wall would meet the floor.

Design and construct your own staircase on a piece of oaktag and use it for the following investigation.
Use a ruler, or T square, and triangle to draw straight lines.
Vocabulary
- The run is horizontal and the distance between the risers.
- The rise is the back of the stair and the height of each step.
Investigate patterns on a stair model
- Measure all the runs on your model.
- Measure all the rises on your model.
- Add all the runs on your model. and record the data in a table.
- Add all the rises on your model.
- What is the distance from the floor to the top step on your model?
- What is the distance from the wall to the front of the bottom step on your model?
- How do these distances compare to the sums of runs and rises.
Summarize patterns discovered in your model.
Investigate patterns on a staircase.
Background information:
On steps there is usually a stair tread that represents the run on the model. Usually the tread is wider than the run. Therefore, the measurement of a stair tread needs to be modified to accurately represent the stair's run.
Use what you know about stairs, select a staircase, collect data for it, and record it in a table.
| Staircase data | |
|---|---|
| Data collector | |
| Stair location | |
| Rise | |
| Tread | |
| Number of steps | |
| Total rise (height) | |
| Total run (depth = run + tread overhang) | |
| Ease to climb | |
Write a formulas for the total rise and run of a staircase.
The higher the rise, the higher a person needs to step.
The lower the rise, the more steps needed in a staircase.
Make a graph or a side view diagram to show the rise and run for each stair in the measured staircase.
How does the step diagram compare with a line graph?
S - Pattern
S pattern
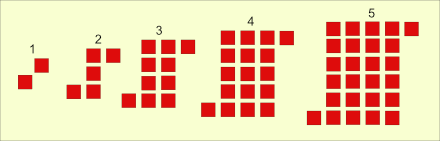
Use the 5 S pattern above and sketch the next two figures.
Use the table below to organize your count of the number of squares in each figure. Could divide each S into top, bottom, & middle OR left, right, & center.
| Figure | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Total |
Describe the pattern you found.
What would be the total number of squares in the 20th figure?
Write a formula to find the total number of squares in any figure of the pattern.
Hints:
- Visualize the addition of squares to complete a large square with side n. One that is (2x2); another (3x3); and (4x4); and (5x5). Then take away the squares that aren't in the pattern.
Should discover ...
[ n2 - 2(n - 1)] - Viusalize two outer squares with a rectangle between them. Then the length times the width of the rectangle in between the two outer squares with the length and width of the sides as n + 1 and n - 1. Then, need to add on the two squares outside the rectangle. Should discover ...
[(n + 1) (n - 1) + 2] - Visualize a square by moving and rotating the top or bottom row. The side of the larger square is n and there is one small square left over.
Should discover ...
[n2 +1)] - Other solutions:
[(n - 1)2 + 2n];
[(n + 1)2 - 2n];
[n(n + 1) - (n - 1)];
Blank graph
