Spinners and probability

Same Spinners Same Numbers

Challenge question

If two spinners are divided equally, numbered with three numbers, will either spinner be more likely than the other to have higher or lower numbers?

Purpose: To investigate equal probability, unequal probability, experimental probability, theoretical probability, tree diagrams, and tables with respect to probability.

Materials: sets of equal spinners with like numbers and unlike numbers (spinners).

Procedure:

Determine:

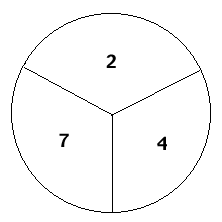
If two players use the same spinner (each spins a 1, 2, 3 spinner).
Determine who would be more likely to spin the smaller or larger number in ten spins?
Experimental probability: Find a partner and play ten games.
Record the outcomes in the table below: (1, 2, 3), and which person has the high or low number or tie.

Is it more likely to spin smaller numbers?

Would this be a fair game?

Why or why not?

Game data:

Game	1	2	3	4	5	6	7	8	9	10	Total
Spinner A. ____________ 1 2 3
High, Low, Tie	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	__ H __ L ___T
Spinner B. ____________ 1 2 3
High, Low, Tie	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	H-L-T	__ H __ L __ T

Share the data with the class and complete the class data table.

Class data for 12 teams:

	Spinner A 1 2 3			Spinner B 1 2 3
	High	Low	Tie	High	Low	Tie
Team 1
Team 2
Team 3
Team 4
Team 5
Team 6
Team 7
Team 8
Team 9
Team 10
Team 11
Team 12
Total

What is your experimental probability?

What is the class's experimental probability?

Theoretical probability: Use the tree diagram to determine all of the possible outcomes and record them in the tree below.

Possible outcomes tree:

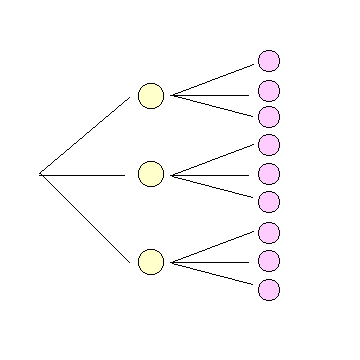	Spinner A 1	Spinner A 2	Spinner A 3
Spinner B 1
Spinner B 2
Spinner B 3

What is the experimental probability?

Hints:

Make an outcome tree!

Possible outcomes for two spinners with three numbers on each spinner!

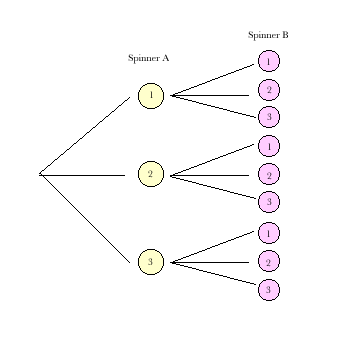	Spinner A 1	Spinner A 2	Spinner A 3
Spinner B 1	1 1 tie	1 2 spinner A	1 3 spinner A
Spinner B 2	1 2 spinner B	2 2 tie	2 3 spinner A
Spinner B 3	3 1 spinner B	2 3 spinner B	3 3 tie

Same Spinners Different Numbers

Purpose: To investigate equal probability, unequal probability, experimental probability, theoretical probability, tree diagrams, and tables with respect to probability.

Materials: sets of equal spinners with like numbers and unlike numbers (spinners).

Procedure

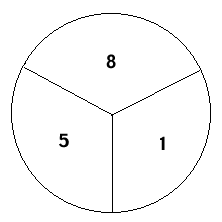
If two players use spinner divided into equal sections, but each has a different set of numbers on the spinner. Who would be more likely to spin the smaller or larger number in ten spins?

Experimental probability:

Find a partner and each spin one of the two different spinners (1, 5, 8 or 2, 4, 7) record the outcomes.

Is it more likely to spin smaller numbers?

Would this be a fair game?

Why or why not?

Game data:

Game	1	2	3	4	5	6	7	8	9	10	Total
spinner 1 5 8
High or Low	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	____ H - ____ L
spinner 2 4 7
High or Low	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	H - L	____ H - ____ L

Share the data with the class and complete the class data table.

Class data for 12 teams:

	Spinner 1 5 8		Spinner 2 4 7
	High	Low	High	Low
Team 1
Team 2
Team 3
Team 4
Team 5
Team 6
Team 7
Team 8
Team 9
Team 10
Team 11
Team 12
Total

What is your experimental probability?

What is the class's experimental probability?

Theoretical probability: Use the tree diagram to determine all of the possible outcomes and record them in the tree below.

Possible outcomes tree:

	Spinner 158 - 1	Spinner 158 - 5	Spinner 158 - 8
Spinner 247 - 2
Spinner 247 - 4
Spinner 247 - 7

What is the experimental probability?

Hints

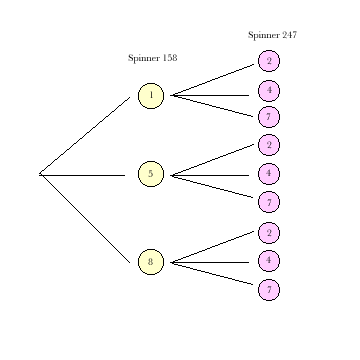	Spinner 158 - 1	Spinner 158 - 5	Spinner 158 - 8
Spinner 247 - 2	2 1 spinner 247	2 5 spinner 158	2 8 spinner 158
Spinner 247 - 4	4 1 spinner 247	4 5 spinner 158	4 8 spinner 158
Spinner 247 - 7	7 1 spinner 247	7 5 spinner 247	7 8 spinner 158

How did you determine experimental probability?

How did you determine theoretical probability?

What is the difference between theoretical probability and experimental probability?

Data sheet or data center

Big ideas and definitions

Probability is how likely it is that a specific event will happen. In math, we find this by writing a ratio (a fraction between 0 and 1).

Before an event (Theoretical): We compare the number of outcomes we are looking for to the total number of all possible outcomes.

After an experiment (Experimental): We compare the number of times the outcome we are looking for actually happened to the total number of times we tried.

Therefore, probability can be determined in one of two ways: theoretical and experimental.

Theory is an idea used to explain or predict an event.
Theoretical probability is determined with reasoning. We look at a situation where all outcomes have an equal chance of happening, and compare the number of outcomes we are looking for to the total number of possible outcomes.
Experiment is a test or set of trials made to try to understand something.
Experimental probability is determined by doing. We repeat a certain event multiple times, collect the results, and find the ratio of the number of times each possible outcome actually happened to the total number of times we tried.

Either way: the probability of an outcome is the number of specific outcomes out of the total number of all possible outcomes for a particular event.

Theoretical Probability =

Number of outcomes we are looking for Total number of all possible outcomes

Experimental Probability =

Number of times the outcome actually happened Total number of times we tried

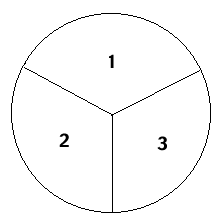
Spinners

Paper clip spinner

Use a paper clip to make a spinner.

Put the smaller end at the center of the circle, so the larger end is toward the edge of the circle.
Put the point of your pen or pencil inside the paper clip on the center of the circle.
Flick the paper clip with your index finger so that it spins around the point.

Purchased spinners

Top

Dr. Robert Sweetland's notes
[Home: homeofbob.com & thehob.net ]