Medial triangles challenges
Questioning is the foundation of all learning.
The first step in rejecting not knowing is to ask, why?
Sweetland
Medial triangle challenges
What are medial triangles?
The information below includes diagrams of medial triangles and focus questions to explore their constructions and relationships!
Hint:
A medial triangle is the triangle formed by connecting the three midpoints of larger triangle.
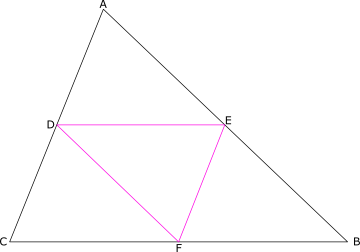
The pink triangle is the medial triangle of the black triangle.
How can you make them?
Focus questions
- How are medial triangles constructed? choose from the following focus questions to guide you. It is okay to skip around.
- How can you bisect a line with a compass? Procedures
- How do you find the midsection of a side of a triangle?
- How can you make a medial triangle?
- Is a medial triangle similar to the original triangle?
- What is the relationship of the original sides to the corresponding sides?
- How does the original triangle relate to the consructed medial triangle or triangles?
- Explore filling a triangle with medial triangles. What relationsips can you determine?
- After you explore making medial triangles, consider what the properties are for the relationship of a medial triangle to the original triangle.
Examples below.
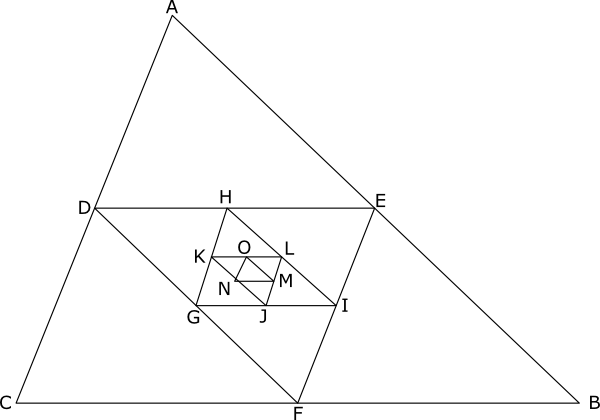
Medial triangle inside a medial triangle challenge ...
Challenge
- Make your own.
- If you continue to make medial triangles, how small can you medial?
- How would you shade them?
Medial triangle inside a medial triangle ... shaded
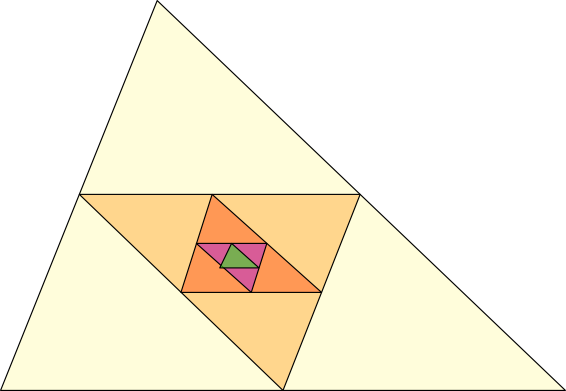
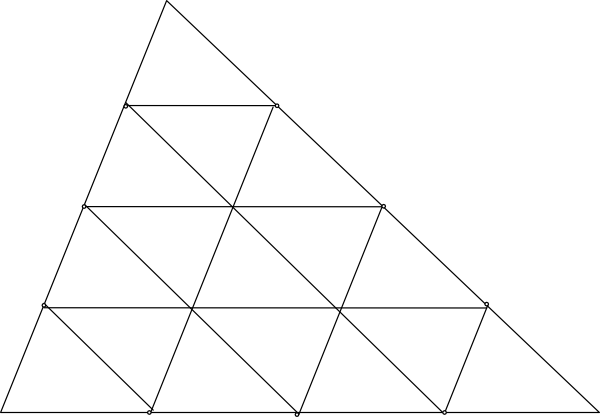
Medial triangle and quadramedial triangles
Challenge
- Make a large triangle.
- Make a medial triangle inside it. Below
- You will have four triangles inside the original triangle.
- Make a medial triangle inside each of the four.
- How many triangles do you have?
- What relationships can you find?
Hint
Medial of a medial
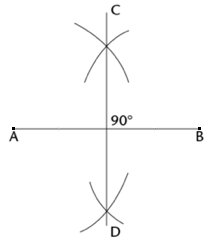
Finding midpoints
- How do you find the midpoint of a line? Place a compass at point A and score an arc above and below the line. Move the compass to point B and score an arc above and below the line. Connect the point of intersection above and below the line to draw a line perpendicular to line AB. It will intersect the line.
- How do you find the midsection of each side of a triangle? Use a compass and score an arc above and below each side from each vertex, connect the points above and below each side, and the line will bisect the side. Continue for each side and mark the midpoint of each side, then connect the points.
- Is a medial triangle similar to the original triangle? They are similar to the original triangle, with a side length ratio of 1:2.
- What is the relationship of the original side to its corresponding side? The sides are parallel to the original triangle's corresponding sides.
- How does the consruction relate to the triangles it creates? It creates four smaller triangles that are all congruent.
Summary of properties

The pink triangle is the medial triangle of the black triangle.
Properties for their relationships include:
- Property 1: Each side of ▵ DEF is parallel to the corresponding side of ▵ ABC.
- Property 2: The length of each side of ▵ DEF is half the length of the corresponding side of
▵ ABC. - Property 3: Triangle DEF is congruent to each of the other three triangles (▵AFE, ▵FBD, and ▵EDC).
- Property 4: The area of ▵DEF is one-fourth the area of ▵ABC.
- Property 5: Triangle DEF is similar to ▵ABC with scale factor 1/2. That is, DE/AB = DFIAC
= EF/BC = 1/2. - Property 6: The perimeter of ▵DEF is one-half the perimeter of ▵ABC.
- Property 7: The centroid of ▵DEF is the centroid of ▵ABC.