Learning Theory & the Development of Reasoning from Infant - Adult
Learning Theory from play to formal reasoning
Play is the highest form of research.
Albert Einstein
The most important factor influencing learning is what the learner already knows and that the job of the teacher is to ascertain this and teach accordingly.
David Ausubel, 1968 Educational psychology: A cognitive view.
- Learning theory
- Introduction
- Play - the best form of learning
- Learning cycle or procedure
- Learning variables- similarities & differences
- Explanations for misconceptions
- Emotional affects on learning & decision making
- Physical activities to develop intelligence, logic, and thinking
- Developmentally appropriate
- Development Of Reasoning
- Development by ages
Introduction
All learning theories are heavily influenced by Jean Piaget's investigations of human development. Probably no other theory has undergone such scrutiny and verification than his ideas for the development of mathematico-logical reasoning. Particularly with respect to conservation and formal operational thinking.
Questions with respect to the generalization of his ideas from research on his children to the world's population have been repeatedly investigated with virtually every culture on Earth with all attempts to find counter examples being generally unsuccessful. Further, his theory and subsequent studies have refuted Bruner's claim that anyone can learn anything at any age if it is presented to them in an appropriate instructional sequence. We must understand that savants achievements are not proof of what we should expect for everyone.
Play and development
Play is central to learning. It is often a spontaneous hands-on activity that has an elements of exploration, tinkering, and inquiry with active, iterative, joyful, meaningful engagement, that sometimes includes social interactions.
Play can be directed in three general ways.
- Free play which is self-directed and regulated. Infants self exploration, children alone with toys or a empty box, toy cooking center, blocks, stuffed animals, dolls, ...
- Guided play is learner directed and regulated with guidance suggested from others (learners, parents, teachers …) based on the learner's initiation and interactions. Offering a toy, or materials to a child, puzzle, building materials, learning centers, menu of choices, do it yourself projects, ...
- Directed play is an activity that is suggested and directed by another person in which the players become engaged in a playful, active, and meaningful manner. Classroom instruction, teaching units, ...
Play's framework is cause and effect, trial and error, notice and wonder all with reflection for further action.
Considering the elements of play is important to understand the kinds of engagement children required for learning.
For example as children play they think deeply about concepts and content since the materials and activities interest them and they are in an environment surrounded by people they trust so they can try out their ideas without fear of making mistakes and failure. People who care and listen attentively to their ideas as they share their thoughts and will support them as they develop their voice and agency.
Infants engage in play from birth. As they do they begin learning by constructing and storing perceptual memories of their sensory experiences while interacting with their environment, play.
These memories are stored in different areas of their brains relative to how they are being sensed and how they are being acted on by the brain. A process which structures information as determined by the types of sensory input, previous memories, the brain's anatomy, and genetically programmed development to create mental schema. Development that enables our brains to make associations and construct better mental schema, structures, actions and operations for thinking, understanding, and reasoning as we adapt to our environment, beginning as play and continuing throughout life as we notice and wonder. These interactions and the memories they create a foundation of dispositions and learning skills for how they will approach and participate in learning in their life.
Since playful exploration initiates learning, it seems logical to know more about how we might create environments and instructional methods and procedures to foster continual learning to develop the abilities for productive learning and a love of learning. This is supported in Research as summarized in A New Path to Education Reform: Playful Learning Promotes 21st Century Skills in Schools & Beyond by the Brookings Institute.
This article describes how educators can provide an environment and practices that meet learner's needs in a playful manner by describing a learning process for how people learn, develop, and use their intelligences, knowledge, and reasoning. It describes how reasoning and emotions can mislead children and adults. But how over time it can develop and become more rational and logical; resulting in increased knowledge and intelligences for better understanding that will motivate learning in specific situations, but learning about how to be a productive learner to achieve our desired goals, which can be approached as playing with ideas at different levels of play.
 Source
Source Learning and development
Learning causes development through learning cycles. Learning processes, which are repeated over and over again as a person matures and gains intelligences and adaptability as new knowledge is structured and connected to previous understandings. Let's review this process and its variables.
Learning procedure or cycle of learning
Let's take a close look at the learning process or cycle of learning.
It starts with a person playing or cruising through life, in equilibrium.
Remember a working memory loves consistency, clarity, and harmony.
When wow!
An event happens that gives the working memory, a double take, cognitive dissonance. When something seems different or doesn't make sense and the person becomes, disequilibrated.
The person has two choices: they can ignore it, no learning, or focus on it and figure out what the heck is going on, learning.
Reflecting on the situation, accessing conscious and unconscious information the situation can be explored and acted on in different ways, with different actions and operations. If none fits with current understandings, or any makes more sense, than what is already known, then the information is remembered and connected to their previous information, assimilated.
However, if a new action, or way of operating on the information, in the disequilibrating event, makes more sense, then a new action, operation, concept, generalization, structure, system ... is constructed, learned - accommodated.
Learned, not in isolation, but influenced by the situation of its creation. Which in turn influences how it will be remembered by the social, emotional, and cognitive sensory inputs at the time and how the brain responds to them, both consciously and unconsciously.
An essential part of a response is how the information is organized, which can be influenced consciously and unconsciously.
- Unconsciously, by intuitive emotional reactions, past experiences, and other subconscious responses.
- Consciously, by playing with ideas and seeing how they can be extended, applied, and changed. Testing the limits of the information for greater benefit. And recognizing benefits. Benefits of understanding the world, adapting to better ourselves, surviving, thriving, and developing of our self-efficacy to live a life worth living to improve and sustain the world.
- When learning is a conscious exploration and results in accommodation it involves all three areas of memory: working memory, short term memory, and long term memory. These areas as studied in a learning brain can be associated with the default mode network, salience network, executive control network, and the brain stem as shown by researchers with brain imaging. See transcendent thinking.

As a person repeatedly experiences the world they cycle through learning cycles.
They learn, develop knowledge, and attain greater levels of intelligences or wisdom.
The process doesn't change, but what we learn and how we know does change.
It is these differences that cause people to claim, all people learn differently.
Which is true, with respects to what is attended to, what is learned, the time frame in which it is learned, and how information is connected or structured.
However, the fundamental learning process does not change.
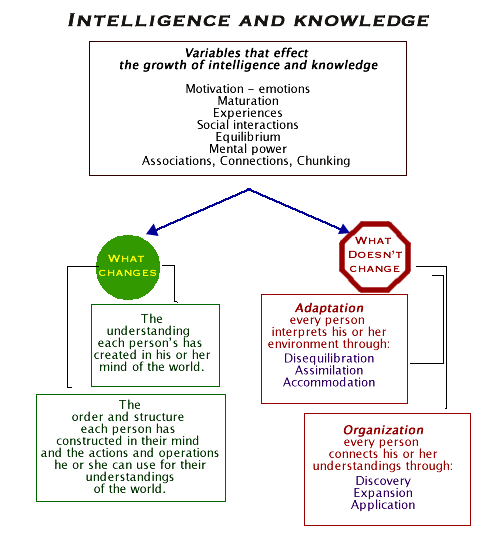
The following chart identifies variables that affect growth and intelligence. And categorizes them as those that change and those that do not change.
It is the general unchanging learning process and knowledge of these variables that affect learning that provides educators methods and strategies to use as a powerful guides to facilitate learning. Outstanding educators are skilled at organizing learning environments by considering how variables, which do effect learning, are best manipulated in learning experiences, or tasks, to invoke a learning cycle that facilitates learning. See pedagogy.
However helpful knowing all this is, there still is significant variability that makes learning a personal activity. So personal that group instruction and mass schooling often fails for even the best educators and learners.
Explanations for misconceptions or learner's thinking as naive understandings
Introduction
We strive to understanding misconceptions to identify each learners' existing knowledge so we might establish a foundation for cognitive engagement and provide opportunities for further deepening their understanding.
Here is a real life experience, as told to me, to illustrate how probing a person's understanding can be a learning experience for the expert and the novice.
Yesterday, I was having some work done at the Ford dealer. A woman, Blonde, if that makes a difference, from Ergon Energy came in and asked for a seven-hundred-ten. The mechanic and parts deptartment representative all looked at each other, and the mechanic asked, "What is a seven-hundred-ten?"
The Lady replied, "You know, the little piece in the middle of the engine, I lost it and need a new one."
The mechanic gave the woman a piece of paper and a pen and asked her to draw what the piece looked like. She drew a circle and in the middle of it wrote 710. He then took her over to another car which had the hood up and asked, "Is there a 710 on this car?"
She pointed and said, "Of course, its right there." Look below to learn what a 710 is.

Once these misconceptions are recognized, it is unproductive to focus solely on their lack of knowledge; instead, it is more effective to concentrate on their current conceptualizations as a starting point for their continuous learning journey.
As we explore diverse learning styles, we expand our knowledge base by uncovering various ways individuals employ logical reasoning and thought processes to transition from less accurate to more accurate interpretations of the world. These strategies are often shaped by their sensory experiences and developmental stage. However, these strategies are limited by the quantity and diversity of their experiences, which are influenced by their current logical and reasoning abilities at the time of each encounter.
Along with these ideas a constructivist-based learning theory is a valuable framework for explaining a developmental trajectory that progresses from illogical to logical explanations of the world.
This section delves into the characteristics of prevalent errors in reasoning and logic.
Misconception causes
Initially, children perceive reality through their sensory inputs (perceptions), which are direct observations of the world (their reality). They are unaware that perceptual senses construct representations of external objects, events, and ideas to act upon and make various decisions. These decisions range from basic, instinctual responses to complex, conscious decisions involving reasoning and problem-solving. All of these decisions are based on sensory input, emotional reactions, learned experiences, predictions of future outcomes, and social interactions in different proportions.
Eventually, children begin to identify inconsistencies in their reasoning, which adults sometimes refer to as misconceptions or naive understandings.
These understandings arise from a limited repertoire of actions, operations, conservation skills, classification skills, and logical reasoning to explain their experiences. Consequently, younger children rely on their internal sensory perceptions to directly reason with the objects and their properties they sense. They establish associations to connect reasonable ideas as explanations for their experiences. These associations often involve comparing their internal perception to another with an analogy to derive explanations, which can lead to illogical conclusions. Examples include:
- Animistic or Animism - speaking as if natural phenomena, living and non living things are alive or have a soul. Explanation as supernatural. God did it.
- Anthropomorphic or Anthropomorphism - speaking as if natural phenomena, living and non human living organisms have human motivations, characteristics, or behaviors. Explanation as a human reasons for doing it or similar act. The light quit working, because it was tired.
- Artificialism - speak as if a human, or conscious entity, created something not nature or is something natural. Thunder is bowling.
- Social - experiences in the world with family, friends, neighbors, TV, mass media, school, libraries, museums, shopping malls, are connected as explanations.
- Oral language - repeat phrases they hear as explanations without understanding.
- Written language - repeat ideas from what they have read as explanations
- Vocabulary - misuse of words as explanations without understanding.
- Metaphorically - use of a metaphor to explain. The sun is like a fire.
- Episodic - explanations that relate to an idea or to a previous event or a particular context, but are not explanatory or causal.
The more experiences a person has in exploring and explaining their world, the greater the information and operations each person has access to, to more accurately explain their world. All dependent on observational evidence processed with logical reasoning of their observations and organized to create reasonable explanations for which they can feel confident.
Emotional affects on learning, decision making, logic and other thinking skills
We must be able to understand and control our emotions for us to accurately represent our world and cooperate for a good life.
Emotions are our natural instinctive inclinations created by our circumstances to prepare us for a response. Circumstances from our internal states and our social and physical environment. They control and influence everything we think, know, and do. While in our hunter-gatherer times our ancestors survived with a quick response, today emotional control benefits us more. Therefore, understanding how the brain works, our emotions, and how we express them to bring intelligence to our emotions and a civility of caring for ourself and others in our life is much more beneficial.
Emotions influence all decisions. Starting with how we interpret our sensory perceptions, what we focus on, what we choose to act on, and the behavioral responses we choose to achieve our goals.
Responses initially stimulated by our sensory inputs register in our brains, which cause an initial release of hormones within our bodies. After this initial response, our mental and physical responses continue to determine the kinds and amounts of hormones which will continue to be produced and affect our decisions. We might be caught off guard and respond reflexively with a fight, flight, or hide response. Which we could escalate to a fear response or relax and extinguish the perceived threat and change the type and quality of hormones within our body accordingly.
Since everything we do is based on emotions, and it is apparent the power of emotions is shortsighted, then we must consider their effect on our desires, motivation, decision making, learning, behavior, and communication which can be laced with bias and propaganda. Let’s review some considerations:
Considerations related to emotions, learning and decision making (Source)
- First, it is helpful to recognize that the decision making process is often hijacked, by our emotions. And we often value our emotional feeling responses over thoughtful reason based decisions.
- We over estimate our ability to make rational decisions and how often we believe a purely rational argument will influence people’s decision making. When we do so, we often neglect to realize how emotions take over, intelligence is put on hold, and passions overcome reason time after time.
- When we rely more on emotional decisions than mastery oriented decisions, we are biased.
- Bias is a systematic pattern of deviation from a sound logical decision or judgment.
- Individuals create their own subjective reality from their perception of the input.
- An individual's construction of reality, not the objective input, may dictate their behavior in the world. Thus, cognitive biases may sometimes lead to perceptual distortion, inaccurate judgment, illogical interpretation, or what is broadly called irrationality.
- Once an image or idea gets into a brain it will stay there and its influence will vary.
- Bias can influence forever if you let it.
- We overvalue fear.
- Emotions are strengthened with the use of hormones (serotonin, dopamine, oxytocin, adrenaline, …) as the brain responds to stimulus.
- Responses from different parts of the brain vary. Response to act that are more reflex or emotional decisions are made closer to the brainstem with more reasonable and logical decisions made closer to the cerebral cortex. Examples:
- Brainstem controls basic automatic and unconscious actions such as breathing and involuntary movements.
- Midbrain coordinates sensory processing and passes that information up the brain. Limbic system makes emotional responses, attention, formation of memories, and the fight, flight, or or hide response.
- Cerebral cortex makes the most sophisticated processes of thinking, planning, and implementation of planned actions. Where critical thinking, analysis, and checking of emotional actions can happen.
- Our perceptions and actions are also influenced by our emotions at any time, whether we are relaxed, in the zone or flow (ZPD), or stressed. When we are in the zone or flow we are doing something smoothly, continuously, and effortlessly. Elements to attain flow include:
- Competence and control,
- Appropriate level of challenge,
- Clear goals and feedback, and
- A focus on the immediate. (Or how to make a viral video)
- Different cultures express emotions in different ways with different words and expressions. And we all express emotions differently on different occasions. In addition to expressing them differently we also can interpret the same feelings in different ways depending on the occasion. An increased heart rate, sweat, … can be interpreted as stress, anxiety, and exercise.
- Our interpretation also depends on individual experiences, culture, brain wiring, genetics, social situation, physical activity, metabolism, emotional experiences, and perceptions of others. The brain feels all of this and without a conscious decision with the frontal lobe, we will not distinguish between reality or imagination and suggest ideas which may or may not be dumb. Ideas which can result in actions to achieve what the brain desires: excitement, pleasure, or something else, without understanding or even considering the consequences or dangers, in spite of our best intentions.
- The younger we are, the more likely bad emotional decisions will be made.
While emotions are culturally influenced, we believe they can be individually controlled. With our ability to control them getting better as we mature. As we discover that emotions come first and what we do follows them, giving us a choice to take actions, which is sometimes easier to say than do. However, through experience we can learn to recognize our feelings, where they originate, and learn how to recognize and manage our emotions along with ways to recognize the difference between fact and emotions.
Information in this article focus on learning Review intuition and reasoning for and moral and ethical development.
An example that to recognizes the difference between fact and emotions
Suppose a learner complains to a teacher's decision by saying, "That isn't fair!"
The teacher responds with a true statement: "Life isn't fair."
And the learner gets angry, because they were hoping the teacher would make a different decision.
The learner's response is emotional, not logical, as it is true, life isn't fair sometimes.
The learner makes a big deal of it, goes home and complains to their parents, who make a big deal of it, and so on and so forth…
Bottom line. It's totally acceptable to tell a middle level or above student life isn't fair.
No one should disrespect a teacher for a reasonable response when the real issue is the student's response.
One might object, based on, the teacher should have been more sensitive and inquired as to what was perceived as unfair … Well … YES! Maybe!
The point is: what is the reason for the learner's anger?
Not the anger itself.
Surely one shouldn't have harsh criticism for stating a fact. The student and parent are misdirecting their energy. If their purpose is to help their child, their goal should be to discover why the child would be upset and have an emotional response for a statement of a simple fact! That is a problem for which a solution would have greater benefits for the student; instead of seeking revenge on the teacher making a true statement and ignoring the learner's inability to deal successfully with their emotions.
This is a problem similar to political correctness, since correctness is based on a person's feelings of being offended, which the person, bases on their personal emotional response to their biased perceptions. Therefore, the focus is on the emotional feelings instead of the actual situation.
The real question to ask is.
Was the attempt of saying, life isn't fair, a valid attempt to help the learner forget, refocus, and move on? Or was it an attempt to use emotions to gain power over the student and control them for unhealthy purposes? Like advertising, fake news, propaganda, bias, brain washing, cults, … ?
Information that follows describes physical activity of children related to learning and they develop from birth to adult.
Transcendent thinking
The ultimate goal of learning is transcendent thinking as described by Mary Helen Immordino - Yang in, The Power of the Adolescent Brain and Mind. in Kappan, Summer 2025.
In this article she describes how the learning cycle, motivation, and learning are supported by brain research and explores the unique cognitive and emotional development that are achieved during adolescence with these processes. She emphasizes the adolescent brain's capacity for formal thinking, self-reflection, and emotional depth, which are crucial for identity formation and moral reasoning. The piece also discusses how these developments impact learning and behavior, highlighting the importance of supportive environments during this critical period.

Transcendent thinking involves coordinating different brain networks: those involved in effortful, focused thinking and those involved in internal reflection and free-form thinking. This happens under conditions of strong emotional engagement.
- The executive control network manages focused, goal-directed thinking and action, keeping the thinker on task.
- The default mode network activates during relaxation and free thinking, engaging in open-ended reflections that transcend the concrete. It's crucial for morality, identity, and social emotions like compassion, gratitude, and admiration for virtue. It trades off with the executive control network, which is generally inactive simultaneously.
- The salience network senses internal body states and manages physiological arousal, alerting us to physical sensations and important stimuli. It weighs information relevance and steers attention to what matters. Centrally connected network hubs facilitate the toggling of other brain networks' activity, fueling motivation and driving thinking about important and compelling things.
- Deep emotional engagement is associated with brain-stem activity, which is essential for consciousness and regulating life processes like breathing and heart rate.
Physical activities to develop intelligences, logic and other thinking skills
A person does not know from what one senses (observes).
When a person perceives, internalizes, and constructs knowledge; that construction requires action on objects and ideas. For young children those actions occur as play. To know an object, requires the child explore it and act on it. Actions that physical manipulate their world and the object within it; to learn about them, their properties, and any changes from their interactions. Additionally they learn how to think. How to construct and use actions, operations, reason, logic and other thinking skills to develop their intelligences.
Physical actions support concrete learning. During play, learners manipulate objects and are provided immediate consistent feedback to reinforce learning with and about physical objects sensed through our sensory inputs. It is out there to learn about, it is exploring objects and their properties. Physical properties that make objects unique. Physical properties such as rocks: hard, smooth, rough, hot, cold, and irregular shape which is hard to change. Physical properties of Mom: she is soft, warm, comforting, provides food, and comes when I cry.
Logic and mathematical knowledge is not discovered, it is constructed. For the child it does not exist before it is constructed by the child. Numbers do not exist. They are invented, with the invention tied to the objects. Physical and logical knowledge is necessary to create the understanding of a number system. The idea that mom will come when I call. The idea that eight objects can be rearranged and still have a cardinality of eight. Both of these illustrate how the physical and logical-mathematical are tied together.
The physical knowledge of rocks can be discovered. They are separate objects that can be moved and maintain their shape, mass, color ... no matter in what position they are placed. Mathematical knowledge about them has to be constructed. A number can be assigned to each object in a one-to-one correspondence and the final number assigned, is eight, no matter how the objects are moved (in one pocket or two) or which gets assigned which number.
Sufficient physical skill, and opportunities to play, provide children with the experience needed to construct all understanding: physical, emotional, social, logical, aesthetic, and any other classification of understandings. The following actions and uses of those actions in play activities are used to create their foundation for learning.
| Action | Use | Play Activity |
|---|---|---|
| Pushing | Slide, Roll, Jump, Skip, Walk, Run, Hop, Throw, Splash, Spill, Smash, Mash, Throw, Press, Scratch, Pluck, Shout, Blow | Water play, blocks, toys, sandbox |
| Pulling | Slide, Roll, Lift, Splash, Spill, Squeeze, Smash, Mash, Suck, | Water play, blocks, toys, sandbox |
| Balance | Hold, Drop, Stop, Still | Water play, stacking, toys, balance beam, swing, building activities |
| Balance and Push and Pull | Support, Carry, Pour, Wet, Water, Fill, Empty, Stir, Mix, Soak, Rip, Open, Dig, Shake, | Water play, balance beam, swing, sand box |
| Smell | Sniff, waft, | Food, flowers, perfume, spices |
| Listen | Hear | Music, stories, talk, video, plays |
| Taste | Lick, | Eating |
| See | Observe | Pictures, video, real life, drawings |
| Talk | Shout, Cry, Giggle, Whine, Whisper, Hiccup | Stories, information giving |
Information that follows describes characteristics of children as they develop from birth to adult.
Developmentally appropriate
Developmentally appropriate practices as described by the National Association for the Education of Young Children.
Nine principles of developmentally appropriate practice
by the National Association for the Education of Young Children. 2020
- Development processes reflect an interplay between biology and environment.
- Domains of development both support and are supported by the others.
- Play promotes joyful learning.
- Variations due to cultural contexts, experiences, and individual differences matter.
- Children are active learners.
- Children’s motivation to learn is increased when their learning environment fosters their sense of belonging, purpose, and agency.
- Children learn in an integrated fashion that cuts across academic disciplines or subjects areas.
- Development and learning advance when children are challenged to achieve at a level just beyond their current mastery.
- Technology and interactive media can be valuable tools for supporting children’s development and learning.
Development of reasoning
Children begin their construction of reasoning with direct observation and comparison of one observation to another. The consequences of reasoning with and about their perceptual senses creates a belief that what is being observed is reality, rather than a construction from their perceptual senses of external objects, which are represented as thoughts in our brains. The result, is not being aware that sensory information can be inaccurate. Over time children will learn how some inaccurate sensory information can be corrected by operating on it with reason and logic.
Therefore, children are unaware which of their sensory perceptions are accurate or not and infer all are real. They act on this information as facts and use inferences and reason to create judgments, concepts and generalizations from them. Operating on them with actions and structures that connect to their mental schema for greater understandings or misunderstandings and misconceptions.
Reasoning can be conscious and unconscious, as our working memory loves peace and clarity, it will seek to maintain harmony with current understandings. However, as more information becomes available, conflicts arise, which can result in change if additional actions create new operations to use in different ways for other explanations and understandings. Operations, which may include: transformations, reversibility, conservation, perspective, classification, order, count, seriate, scale, proportion, relative position, motion, and other actions or operations of reasoning and understanding.
Examples of using perceptions as reality:
- Believing the moon is following them.
- Standing on a railroad track with an internal visual perception of the tracks and thinking the tracks are actually getting smaller and narrowing with distance.
- Thinking pennies are worth more than a dime because they are bigger, or two pennies are worth more than one dime because there are more pennies.
- Thinking five blocks grouped together is less than five blocks spread apart.
- Thinking one wire is shorter than another, because it's bent...
- Illusions and perceptual experiences that challenge reasoning
To correct inaccurate conclusions, learners engage in reasoning by using operations that act on their perceptions. Actions, which may be logical and accurate, but don't have to be. The learner just needs to believe it is. Examples:
- Railroad tracks are an equal distance apart, parallel. They don't get smaller, because when I walk down them they stay the same.
- A set of objects don't change their cardinality if they are moved, because when I count them and move them I get the same count. And besides they are just being moved no objects are being added or taken away. They are the same group.
- Mom and dad are always right, because they say so and I don't know other ways.
- Seven is my lucky number, because when I roll dice I seem to get more sevens than other numbers. Although, sometimes I wish I would get a larger roll.
- Thirteen is unlucky, because I had a bad day on Friday the thirteenth.
- A crystal, stone, buckeye, rabbit's foot, ... will bring good fortune.
- A dream-catcher will keep nightmares away ...
- An apple a day keeps the doctor away ...
- An itchy nose means someone is thinking of me ...
The use of different operations provides learners with experiences to construct and refine their mental actions and operations, such as those, which are needed to conserve.
- Decenter (stop centering their focus on one feature and ignore the relevant others),
- Use reversibility (able to do and undo actions),
- See transformations (able to see change as an infinite series),
- Stop the use of ego thinking, (recognize another point of view, activity in the world is external and perceptions are constructed internally) and
- Stop the use of transductive reasoning (replace faulty reasoning with logical reasoning).
Actions and operations used to explore and adapt to the world. Adaptability created when operations are connected, enlarged, and consolidated to create better mental schema, structures and systems to better understand and navigate the world.
- Activities - directions, materials, & other information to explore mental operations and reasoning
- Discrepant events that challenge reasoning
- Intuited and reasoned judgment for moral and ethical learning
Development characteristics by ages
Birth - age 3 Developmental Characteristics (sensorimotor)
- New borns can suck, grasp, cry, vocalize, move, and grasp to begin their exploration of the world. They will search for food, nipple, after first 20 minutes of life.
- Motion and exploration are random without intention or purpose. Can't differentiate motion of self and objects beyond them.
- New borns can recognize their mother's voice.
- Babies cries are different for different situations: hungry ("na, na" kind of cry is related to sucking), others for tired, ...
- New borns respond to facial expressions.
- Vision is blurred beyond 20 inches for first two months.
- Infants explore and respond with their physical senses (touch, taste, smell, hear, and sight). Can locate the source of sound and coordinate vision with manipulation.
- Will learn better if multiple senses are involved.
- Learn to differentiate objects and follow objects. When they are not sensing or experiencing an object the object is not represented in their mind. Thus adding meaning to phrases, out of site - out of mind. Objects that can't be seen, cease to exist, don't have permanence.
- Can differentiate between one, two, and three objects. And few or many objects.
- Four - eight months they will anticipate the position of moving objects and follow objects after they disappear from view.
- Object permanence - objects, beyond themselves, continue to exist even when they are not being observed (8-12 months) faces, sounds, objects. Before object permanency hiding a bottle doesn't initiate a search, just panic. When an infant has object permanence, they can reverse a bottle to get the nipple and they will search for an object when it is hidden. These changes cause peek-a-boo to progress from startling to fun to boring.
- Must believe objects have permanency, continue to exist, to learn about the world with the belief of what you discover and learn will continue to exist and have meaning. Meaning that is consistent so cause and effect, reason, and logic have value.
- Discover self. Recognize self in mirror at 18 months. Act as if the world revolves around them. May have a temper tantrum when the don't get what they want.
- However, they will comfort others when they are hurt or sick, eager to assist and help others, show empathy and share pain.
- Will babble to communicate and can understand three times more than they can communicate.
- Their skeletons harden, knee caps develop.
- At one year their height has doubled and weigh tripled.
- Twelve - twenty-four months. Object permanence leads to understanding of constancy of size, shape, and other physical properties of objects. This adds stability to mental representations (abstractions) making thinking about inferences for cause and effect about changes observed during exploration and experimentation of their environment.
- Shake rattle causes sound. Pushing and dragging on a touch screen changes the images or causes sounds. Crank the handle, music plays and Jack jumps out of the box.
- Understand movement not perceived, (can predict an objects path if they see it move toward a screen, disappear behind it, and know where it will emerge on other side) and can represent spatial relationships.
Preschool - Second Grade Developmental Characteristics
(preoperational)
The brain interprets the world on a need to know basis; only adding additional information as curiosity and desire push for more exploration to attain more information and detail. The amygdala is involved in deciding how much to process and reacts to stress by processing less information.
- Learn language. Language is deferred imitation. It is never the source of physical or logical-mathematical knowledge with out reference to pre or concrete operations.
- Language can be an obstacle to the development of reasoning and intelligence. Use words without associating meaningful understanding.
- Language slows thought as thinking requires actions to think.
- Language is social arbitrary knowledge. Like physical knowledge it is verified externally, but not with physical knowledge (until children can read and write), but through people or social knowledge.
- Learn vocabulary with a one to one association.
- Simple classification of objects into unique one property categories.
- Can hold one property or variable constant while other variables change.
- Logic is simple one-to-one chained relationships or step by step, one step at a time thinking.
- Can use symbols or mental representations. Therefore, mentally being able to manipulate symbols and mental representations is - abstraction of thought. Symbolic play is when another object can be thought of as another thing or pers0n during play. Blocks become cars and guns. Teddy bears a child or friend. Symbols are entirely arbitrary and generally shared socially. However, they can be unique to an individual child.
- Creates mental images

- Use deferred imitation will repeat the sounds a person says trains and animals make, choo-choo, meow, moo, ... Will repeat actions they view. Play house, doctor, sports, ...
- Likes to Draw. Drawings will be flat 2 dimensional, with some limited detail, and proportion. Will draw what they know, as represented in their mental schema. Not what they see. Example of dragon and knights ...
- Verbal, likes to talk about everything and to everyone, nonstop.
- Use mutual exclusivity and perfect it with one-to-one correspondence. Big Bird example. Big bird is big bird. Can't have another name.
These characteristics are possible largely because of object permanence and being able to construct and manipulate mental representations of objects as they are sensed. Their representations and ability to manipulate or act on their abstractions are contained or limited through the use of the following operations or lack of use of its opposite, which must be constructed for concrete operations.
- Egocentric thinking, believe their view is the truth. Understanding is based on their sensory input. It is not a selfish point of view. They don't recognize that other people may have a different point of view or that another point of view could exist. Inability to differentiate between self and others.
Four and five year olds showed they understood another person's point of view when they were in a room with two other persons. A red ball was put into a box and one of the persons left. While they were gone the other person moved the ball into another box. When young children were asked what the person, that left, would say when they returned about the ball's where abouts, the younger children would answer in the second box. Children between four and five were able to know, that the person who left, had a different point of view and would answer - they will say the ball is in the initial box.
To think critically they need to recognize there are points of view other than their own. What I believe as reality is one way to perceive the world and other people might have a different view. Need to use critical thought, allocentric thought, or sociocentric thought, to differentiate between self and others. To develop, ask questions as to what do you think the other person saw? Why did you pick this one? Why did she pick that one? What did the character in the story think? What did another character in the story think? Why did they think different things? Why did they think the same? Intent is to develop the idea of different points of view. - Reversibility is the inability to reverse a thought. All sensory motor operations, perceptions are basically irreversible. Can't undo senses, can't unsmell, untaste, unsee. Therefore, it can be understood that reversibility is counter intuitive and a mental construct that has to be invented. Like wishful thinking of sometimes wanting to undo time. Reversibility is the ability to work a problem in both directions. Use logic both ways. This is essential to understand the order of events in time. In mathematics the position of an object doesn't change the object or its cardinality as the object can be reversed, transformed, from one position to another and back again.
- Being able to move four objects from one position to another doesn't change the cardinality (the number of objects) as they can be reversed to the original position.
- Being able to imagine water being poured from a measuring cup into a tall narrow container and then from the tall narrow container to a short wide container will have the same amount, because pouring it back into the tall container would reverse the process and the amount would still be the same.
Being able to take two wires of equal length, bend one, set them side by side and mentally reverse the process of unbending the wire to its original length and declaring them to be equal in length. - Knowing that if 3 + 4 = 7 then 7 - 4 = 3 is the reverse process. If you add four and get seven, then if you have seven and remove four the process has been reversed.
- If exercise causes you to breath faster, what could you do to breath slower?
If water makes ice how can it be reversed? - If salt is added to water can it be reversed? If it can, can the salt be reversed again with more water?
- Water evaporation and condensation.
- Balancing activities like those in FOSS for second grade as well as balancing on an equal arm balance.
- Mixing paint and watching the color change. Can paint be made to go from light to dark to light again?
- What about light from a flashlight? If we slowly add slips of waxed paper what happens? What if we remove them one at a time?
- What about unrolling a ball of string? How long is it? If we roll it up and unroll it again how long will it be?
- If you are feeling pretty smug about your ability to use reversibility, then think about being in a market and looking at all the different shapes of containers and trying to identify which are equal or which has more or less. I bet the packaging companies know which containers look like they hold more than they actually do, because of our inability to use reversibility well.
 Uses centering focuses on a characteristic as an explanation or cause, that may or may not be accurate, without consideration of other options. Decentering is the ability to change ones thinking from one characteristic to another when considering an explanation or cause. Able to explore all or multiple variables of an action, operation, idea, or event. Eventually systematically and simultaneously.
Uses centering focuses on a characteristic as an explanation or cause, that may or may not be accurate, without consideration of other options. Decentering is the ability to change ones thinking from one characteristic to another when considering an explanation or cause. Able to explore all or multiple variables of an action, operation, idea, or event. Eventually systematically and simultaneously.- Does not recognize transformations. Transformation is understanding that change can involve an infinite progression of steps, usually incrementally small. However, a progression that becomes infinitely large would be included as well.
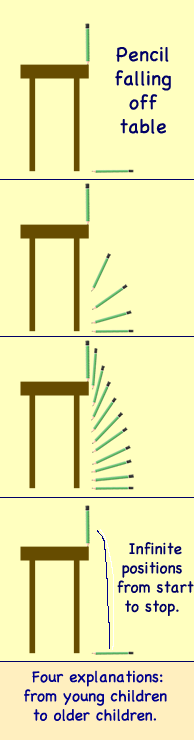
Transformation is a mental structure necessary to be able to conserve. Piaget investigated and wrote about it. In one study children were asked to draw the position of a pencil from the moment it left a table until it hit the ground. He found it took several years for children to construct the idea that the pencil was in an infinite number of positions from starting to fall till landing on the floor.
Transformations are important to understand a concept of variable. Being able to visualize how a variable is changed across a range of possibilities or is infinitely continuous, is necessary for understanding and explaining the world. Continuous as opposed to a series of steps, beginning, middle, end. Like Google map shows a trip with a list of turns rather than a continuous route for the journey. Or a number line as stepping stones across a stream rather than a continuous path across it.
Transformation also applies to moral issues of right and wrong. For example: when the pencil is in the hand (totally right) to the pencil on the floor (totally wrong). However, moral issues can also range from an extreme rightness to extreme wrongness with a continuum of exceptions in between. For example when is it okay to tell a lie? The extreme cases would be: never to always. However, situations such: Do you swear to tell the whole truth ....? Do you like my shirt? How was the dinner I cooked? Suggest the idea of transformation might a strategy to use in discussing moral issues. See also moral and ethical development.
Another example is science. Science takes the view that it can not be proved the pencil will hit the floor every time it is dropped. There are no 100% right answers. Everything is tentative. However, there are certain events or objects where we believe some facts or inferences (theories, laws) are closer to truth than others (99.9%). For example with the seasons. Scientist are pretty much in agreement that the Earth's distance from the Sun doesn't vary enough to cause the seasons. And that the directness of the rays does vary enough to cause the seasons. However, even those ideas are tentative and open to reevaluation if new evidence is discovered. Just because you never saw a purple cow, doesn't mean there is none.
While this idea is not too difficult for adults to understand it is difficult for young people as they are still constructing or assimilating a variety of ways to apply transformations. Then to compound the problem is what seems to be a human obsession of wanting to classify everything as right or wrong; black or white; ying or yang. Of course it isn't easy for teachers either when we are forced to evaluate tentative answers.
Related activities or tasks.- Sequencing objects of different lengths (Piaget's famous dowel rod experiment)
- Drawing pictures of the animation of a pencil or other object falling from a table or hand to the ground. Image to the right shows the progression of development of this idea. Young children draw the pencil standing on the table and laying on the floor. They do not draw the pencil at an incremental position. Later, children will place the pencil between the starting position and its final resting place. However, they will draw more representations toward the final position than the initial position. Eventually they will recognize infinite possible positions and draw many Iillustration3) or label it as such (illustration 4).
- Animation by making flip books
- Mixing paint and watching the color change. Add a little bit more darker paint at a time to lighter or lighter to darker.
- Flying paper airplanes and see how slowly changing the weight (add one paper clip to the nose, fly it five times, measure the distance to the nearest yard or meter, record it, and add another paper clip and repeat till five clips. or fold the ends of the wings a little more at a time and see how it changes the flight.
- Uses transductive reasoning may or may not be accurate. It is usually based on what one has experienced, (concrete properties) and associating one idea from one object to another object or experience. Usually an association related to simultaneous actions without cause and effect or logical reasoning (deductive or inductive). Juxtaposition of reasoning. A leaf is thin and floats so thin objects float. A rock is heavy and sinks so heavy objects sink. Can result in magical thinking, animism, faking connections, and other faulty reason. Reasoning resources.
- Lacks conservation of reasoning - Children in the primary grades must be taught as if they are lacking conservation skills. Anything that involves measurement needs to be experienced in its actual size. If students are studying animals, then the animals need to be drawn, outlined, or traced on sheets of paper to the exact size of a typical animal in the species. When a height or length is referred to, then pieces of string, yarn, or adding machine tape can be used to mark and show the sizes concretely.
- Solar system models create similar complications. A bigger problem with a solar system model is scale. Learners don't begin to develop the abilities for scale until about fourth grade. Then when a solar system model is made the scale for the size of the planets as well as the distance from the Sun need to be similar for an accurate representation, which is complicated as demonstrated when calculating scales for the planet's diameters and distance from the Sun.
- Similarly for time. A timeline can to be drawn with times in increments of the students' lives or generations for their parents and grandparents.
- Drawings are mostly flat two dimensional that lack perspective and scale.
Age 8 - 11, grades 3 - 5 Developmental Characteristics
(Concrete Operational)
- Develop class inclusion - Use classification and generalization to solve problems (all dogs are animals, only some animals are dogs. A tree is not an animal, therefore it is not a dog. A collie is a dog, therefore it is an animal.)
- Develop serial ordering - Arrange a set of objects or data from smallest to largest or by other criteria and create a one-to-one correspondence. Arrange people from smallest to largest and and relate to age.
- Develop conservation ability to question perception and reason about reality. To use logic instead of perception to make determinations for what can appear obvious, but is not. See also conservation task directions, materials, & other notes.
- Conservation of length - Perception of two wires of equal length, a bent wire and a straight wire, suggests the straight wire is longer.
- Conservation of number - five is five no matter if it is five elephants or five mice. No matter if the five horses are gathered by the fence at the barn or if they are spread out across the whole 10 acre field.
- Conservation of liquid/volume - Perception of two drinking glasses, of equal volume, with one being tall and narrow and the second being short and stout, would visually suggests the taller has a greater volume. Abstract reasoning could cause us to represent the two by imagining the tall one shrinking in height as it increases in girth. However, this is hard to do. Teen campers, who after being taught how to judge their serving sizes of beverages were given short wide glasses and tall thin glasses, which held the same volume, to pour their morning juice. They poured an average of 9.7 ounces into the short glasses and 5.5 ounces into the tall glasses. When questioned, they responded they believed they had poured less than 7 ounces into the short glasses and more than 7.5 ounces into the tall glasses. The same experiment was done with 89 adults. Seventy-nine percent of those with short glasses underestimated how much they poured and seventeen percent with tall glasses underestimated. Similarly, bar tenders poured 31.3 percent more into a tumbler than the more slender highball glass: 2.1 ounces v. 1.6 ounces. While these are errors in conservation reasoning, they have big implications for overconsumption of sugary drinks, alcohol and self dosed medications.
- Conservation of solid/mass - a ball of clay will have the same amount of solid material or mass if it is rolled out as a snake, pounded as a pancake or rolled into a ball.
- Conservation of area - My favorite one to act out is a story about two farmers: Mr. Smith and Mrs. Jones. Who have a farm yard with the same amount of grass.
- Mr. Smith and Mrs. Jones. Both have a farm yard with the same amount of grass.
- Place two identical pieces of green construction pieces.
- Ask, Which farm yard has more grass? (neither they are the same.)
- Okay good. Now on with the story.
- Mrs. Jones decides one day that it is time for her farm to grow so she builds a barn ( I place one Monopoly hotel on the green piece of construction paper).
- Mr. Smith, wanting to keep up with the Jones, build a barn exactly the same size ( I place one Monopoly hotel on the other green piece of construction paper).
- The next year Mrs. Smith decides that things are even better and builds two more barns along side of the first barn ( I place two more Monopoly hotels on the green piece of construction paper right beside the first).
- Mr. Smith, again wanting to keep up with the Jones, builds two more barns, but spreads them out across the barn yard ( I place two more Monopoly hotels on the green piece of construction paper so that all three are spread across the page).
- The following year Mrs. Jones has another good year and builds two more barns again side by side her original ( I place two more Monopoly hotel on the green piece of construction paper beside the other three).
- Again Mr. Smith, keeping up with the Jones, builds two more barns only he decides again to build his barns spread out across the farm yard ( I place two more Monopoly hotel on the green piece of construction paper spread apart from each other as much as possible).
- If there are more hotels, I continue until all of them are placed on the green construction paper, making sure to add them equally.
- Then one day Mrs. Jones goes out and buys a cow.
- Mr. Smith, wanting to keep up with the Jones, goes out and buys a cow.
- When both cows are let out into the farm yards, which cow is going to have more grass to eat?
- Most people who have never heard this problem before will have as their first hunch or answer the cow in Mrs. Jone's pasture. Just look at all that green. The image of the red (barns) hotels spread across the green paper and image of the green paper with barns huddled together in a corner can create a preoperational non conservation of area response or Mrs. Jone's cow based on the visual evidence. However, if you are skeptical enough, or whatever, to ask yourself to just wait and think here. You might reason that the amount of green covered by the same number of barn/hotels is equal, therefore, each cow would have the same amount of grass. If you are still not sure, act it out. Or get two pieces of graph paper and pencil in two squares for each barn. On the one sheet color them all in a corner and on the other spread them out. Are they the same area? Is the amount of grass the same? In order to conserve area a person needs to be able to stop their egocentric thinking and reason: Maybe there is a different way to think of this, rather than just looking at the grass for each, decenter (how else can I think about this problem rather than by looking at the amount of green and comparing), transformation (think what would happen if all the spread out barns/hotels started together and were moved/transformed to where they are now) or (what would happen if all the grouped together barns/hotels were moved/transformed to where they are now). It wouldn't matter where they are as they would be still sitting on the same amount of grass. Reversibility - If I can move the barns, they can be spread out, and then, they can be returned rejoined. Egocentric thinking is replaced by logical-mathematic reasoning.

- Develop use of perspective in drawing. Can begin to draw representations of three dimensions in two dimensional sketches and will draw with more accurate scaling. About second or third grade students are fascinated by following a procedure to draw a three dimensional representation of a cube on paper. About fourth grade, students are fascinated with the use of perspective and vanishing points to show perspective in their drawings. However, consistent systematic use will not be maintained until later in a formal operational sense.
- Develop the use of operations - Being able to use these operations enables people to make direct references to familiar objects and actions and explain them with associations. Example garduckals. Using associations allows them to create simple hypotheses, follow step by step directions or explanations, and understand others may have a different point of view or use a different reference point than they have or are using at the present.
- Because concrete operational learners begin with their own concrete experiences and associations, rather than with a formal operation, their abstractions are not as comprehensive and flexible with respect to generalizing less familiar or unfamiliar situations. Hence:
Concrete operational learners can identify some variables that interact with an object or system, but do not use a systematic process to identify them, usually resulting with an insufficient list of variables, and do not consistently plan and hold variables constant that are not manipulated or responding variables. - Knows the difference of observation
and inference and can make inferences from observations, but considers a limited amount of possible inferences for an observation.
May apply a related, but inaccurate procedure or algorithm as a solution to a problem.
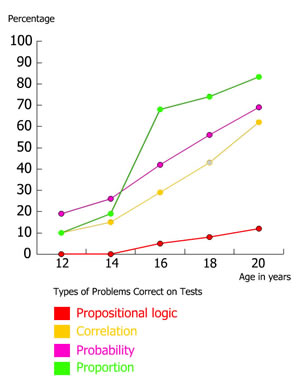
Apply a process without applying his or her own validation of the application of the process against the data, conclusions, or whatever information the situation provides for checking and validating a particular method. - Learners will explore operations and procedures, which are usually indicative of formal operational thought, such as: isolation and controlling of variables, hypothesis, combinations, probability, correlation, proportion, and formal logical reasoning. However, they will do so with concrete objects or drawings that can represent the actual objects being considered and the operations that are being imposed on those objects. It is through these experiences learners are able to think about the operations and with enough experience begin to systematize them so they can become fluent enough to apply them systematically as abstractions. The development of fluent operations, for most learners is well after 12 years of age. See chart below for developmental ages of propositional logic, correlation, probability, and proportion.
Age 11 - adult, sixth grade and up Developmental Characteristics
(formal operational)
How does formal operational thinking fit with the way adults think?
The characteristics of formal operational thought is not just abstract reasoning. Young children (preoperational) use abstractions to connect symbols or other representations to think and reason about real objects or events in their lives.
Formal operational thinking is being able to use abstract reasoning for operations which include more than one direct relationship. It requires reasoning with multiple properties or variables simultaneously, such as propositional logic, correlation, probability, and proportion.
Formal operations implies being able to understand a mental operation or procedure so well that it can be performed on information in an efficient systematical way. Operations and procedures that can be indicative of formal operational thought include isolation and controlling of variables, hypothesis, combinations, probability, correlation, proportion, and formal logical reasoning, which becomes possible at about 11 years old or sixth grade.
Being formal operational for the adolescent means, for the first time in his or her life, they have the mental capacity to think as well as adults and the ability to solve all classes of problems.
While formal operational thinking requires time for the brain to develop; time alone is not sufficient to guarantee formal operational thinking will develop. And one should not assume all adolescents and adults have fully developed formal operations. In fact a majority of adults never advance beyond concrete operational reasoning. See graph with four types of reasoning and scores across age.
While formal operational thinking provides ways of thinking about problems and information comparable to any advanced adult's way of thinking about similar problems; it doesn't mean the number of experiences a person has engaged in during their life time doesn't make a significant difference in their ability and efficiency of solving problems with or without formal operational thinking.
Additionally one may have the ability to use formal operational thinking in one or more particular areas and still not be able to generalize or transfer that formal operational knowledge to other areas. Hence, they rely on concrete operational thinking in those areas.
What does it mean to be formal operational?
Piaget claimed that after the development of formal operations any gain in a person's reasoning abilities is with respect to a person's ability and experiences with the use of logical operations and the efficacy of the individual's mental schema constructed with logical operations and the number of meaningful experiences the individual can associate with the use of the specific logical operations or combinations of those operations.
In other words, there is no higher level of reasoning beyond formal operational thinking. Differences in reasoning among formal operational thinkers is based on their mental power of short term memory, construction of accurate logical procedures, ability to mentally manipulate information from one form to another using an appropriate procedure, and creativity or flexibility achieved by experience to recognize what procedure fits in a particular situation.
Formal thought and concrete thought are similar in that they both use logical operations. However, there is a clear difference in the greater range of reasoning with the type of logical operations used at a higher level of understanding, described as formal operational thinking. A level of understanding, described as concrete thinking lacks systematic analysis, depth and range of comprehensive power, imagination, and flexibility of reasoning. In addition a formal operational thinker is aware logically derived conclusions have a validity different than conclusions directly derived from only facts and observations.
Formal operational thinking characteristics:
- Work with complex verbal propositional reasoning that is not tied to a personal past or present experience.
- Reasoning about hypothetical problems - reasoning that is not tied to a personal past or present experience and can project into the future without being tied to a personal past or present experience.
- Use theories, models, and hypotheses to create solutions to problems. Hypothetical reasoning goes beyond the confines of everyday experience to things for which we have no experience. Reasoning beyond perception and memory about things which we have no direct knowledge. Young adolescents with formal operations can reason about hypothetical problems entirely symbolically in their minds and can deduce logical conclusions.
- Think about his or her own thoughts and feelings (metacognition) as if they were objects.
- Reasoning can be independent of content. Can argue on the logic of an argument (solution or problem) independent of its content.
- Complex problems can be dealt with simultaneously and systematically by coordinating multiple thinking and reasoning strategies and or variables to derive solutions.
- Use inductive reasoning by combining similar solutions to create generalizations, principles, models, and theories.
- Have a highly developed understanding of causation.
- Use deductive reasoning. The use of a premise to create conclusions or the use of general ideas to create specific ideas. Inferences or conclusions created with deductive reasoning are true only if the premises used to create them are true. However, reasoning can use false premises and create logical conclusions.
- Use hypothetical deductive reasoning or reasoning with the use of a hypothetical premises (rather than facts) to create conclusions.
- Combinatorial reasoning is thinking that systematically considers all possible relations of experimental or theoretical conditions, even though some may not be realistic.
- Identify and control all variables when attempting to validate a relationship or inference. Designs a test that controls all variables, but the one being investigated.
- Use proportional reasoning
- Use probabilistic reasoning
- Use correlation reasoning to recognize a comparison between the number of confirming and disconfirming cases of a hypothesized relationship to the total number of cases.
These understandings combine to enable an individual to accept an hypothesized statement or assumption as a starting point for reasoning about a situation. He or she is able to reason hypothetic-deductively. OR... Able to imagine all possible relationships between the variables, deduce the consequences of those relationships, then empirically verify which of those consequences, in fact occurs. Daniella in the transportation puzzle demonstrates this.
Sample questions to apply and discuss what you know about human development
Directions
Discuss how each problem might or might not be solved at the different levels: sensorimotor, preoperational, concrete, formal operational.
- A < B; B < C what is A compared to C?
- Chris is left of Sam and Sam is left of Ben, Where is Chris in relationship to Ben?
- Formal operational can solve this problem in this form.
- Concrete operational can not. However, they can if they create the relationship concretely, draw and label pictures.
- Suppose snow is black?
- Young children will respond with, snow isn't black and possible not want to entertain an argument based on a false premise.
- Older children might think a false premise can be taken as a hypothetical situation that is interesting to speculate about and come to logical conclusions that can be inferred from the hypothetical situation.
- Formal operational, can reason logically or analyze the structure of an argument, independent of the truth or falseness of its content. How does the definition of formal operation relate to the two responses?
- Understand relationships between multiple variables simultaneously. Given an equal arm balance constructed so that the weights can be hung at equal increments from the center if three weights of the same mass are placed six units from the center how many weights of equal mass have to be placed three units on the opposite side to balance?
- Control multiple variables. Students are given the following equipment and asked to investigate and find what effect the kind of material, the thickness of the material, and the length of the material have on the flexibility of the material. Equipment: thick rods of aluminum and wood, medium rods of aluminum, steel, and wood, thin rods of wood and steel. All rods are the same length about 25 cm.
- Understand correlation. Example: What is the correlation of the number with blonde hair and blue eyes and the number with brunette hair and brown eyes?
- A random sample of 100 people is selected. They are surveyed, counted, and classified. Information resulted in the number with blonde hair and blue eyes; the number with brunette hair and brown eyes; the number with brown eyes and blond hair; the number with blue eyes and brown hair. The non-matching pairs were subtracted from the matching pairs and then compared to the total number in the sample. If the comparison is by division, then the result will be from 0 to 1 for a positive correlation and from a -1 to 0 for a negative correlation. With +1 resulting from a sample where all have blonde/blue or brown/brown matches or the entire sample correlates with the hypothesis. With a -1 resulting from a sample where all have blonde/brown or brown/blue matches, or the entire sample doesn't correlate with the hypothesis. Or with 50 50 resulting in a correlation of zero or no correlation with the hypothesis.).
Home: Pedagogy - theory, curriculum, learning, human development, & teaching