Development of fractions, decimals, percent, ratio, proportion, their operations, and connections
Page Overview:
Fractions:
- What are fractions
- Comparing fractions
- Equivalent fractions
- Addition & subtraction
- Developing a connection between multiplication & division of fractions
- Partitive
- Quotative & measurement
- Strategies for solving addition & subtraction of fractions
- Strategies for solving multiplication & division
Decimal & percents
Introduction
This page describes the development of the understanding of fractions, decimals, percents, ratio, proportion, and operations with them. Understanding of these kinds of numbers and relationships requires a fundamental understanding of number values. Understanding, which does not have to be complete, but an understanding within the range of the numbers being used to represent the values and relationships in the situtation to be understood and communicated. Young learners can develop a limited understanding of halves, pennies, and 100% before developing a good understanding of whole numbers into the hundreds.
Background information:
- Number value development
- Development of place value
- Types of numbers fact sheet
- Number line overview
- How to say, read, write numbers lesson plan
Development of Fractions
What are fractions?
A fraction is a relationship of parts to a whole expressed as division and multiplication with a numerator and denominator.
- Fractions are unsolved division problems. 3/5, three divided by five.
- Fractions are equal parts of a whole. 3/5, three equal parts of a whole ...
- Fractions are multiplication and division. 3/5 are a whole divided into fifths and one-fifth multiplied three times.
Young learners assign a fractional value to a part, without systematic reference of the part's values. For example, they may associate one-half to any part of a whole.
Before young learners conserve area they explore different shapes visually and determine, which are identical and equivalent with visual comparisons. Identical shapes are more accurately compared than those, which are not. The harder it is to compare shapes or parts of shapes by fitting them together visually, then the less accurate they will be. However, many experiences are necessary for students to develop accurate operations to verify or refute visual evidence.
For example: Experiences to spatially determine how two identical shapes can fit into a larger shape. A square can be made with identical rectangles (each 1/2 of the square), two identical triangles (each 1/2 of the square). Concretely at first, and then perceptually manipulating pattern blocks, cutting paper, or folding paper to explore size relationships and how to communicate those relationships.
Discovering how many objects it takes to complete a larger shape entirely, are beginning experiences for young learners to identify the number of cubes required to cover a certain area, which are later used to understand and communicate fractional parts. The number of smaller objects to cover a larger area, becomes the part and the larger area, becomes the whole. Thus, initial experiences with whole numbers, can develop into applications with fractions. One of two tiles can represent 1/2, one of three tiles ... 1/3, & one of four ... 1/4. Where the relationship of one object in two is 1/2 of the two, or group, and these concrete representations help beginning learners to develop their spatial abilities to understand fractions. However, there is much development that is necessary to interchange fractional ideas and link them to the fundamental idea of a fraction as division.
These activities also help learners develop spatial abilities to rotate and flip shapes and objects to identify fractional parts in more complicated representations.
Learners need many experiences representing fractions in multiple ways: concrete objects, models, pictures, diagrams, words (written and oral), act out, symbols with multiple objects. See instructional ideas, activities, & assessment to develop understanding of fractional values
As learners explore shapes as parts of other shapes, fractional relationships, or parts of a whole are developed and can be communicated as divisions.
Comparing fractions
Learners initially consider the larger of the numbers (numerator or denominator) in a fraction to determine the larger fractions. Later they will develop accurate algorithms as comparisons become more complex. Algorithms such as:
- If the denominators are the same number, then the denominators are equal, they will compare numerators. For example: 2/3 compared to 1/3. Thirds are the same and two is twice one, therefore 2/3 > 1/3. Learners who do this, may or may not understand the fractional parts are also related to the same or equivalent whole or unit.
- If the numerators are the same numbers, then the numerators are equal and the denominators can be compared to a whole.
- Example 1: 2/3 compared to 2/5. The numerators are the same so compare thirds and fifths to a whole. Thirds are more than fifths, therefore, 2/3 > 2/5.
- Example 2: Compare 1/3 to 1/4 to 1/2. The numerators are all the same so when the denominators are compared to a whole, fourths are smaller than thirds, and both are smaller than halfs. Therefore, 1/4 < 1/3 < 1/2.
- Neither the numerators or denominators are the same. 2/3 & 4/5. They must be compared using the same whole so make the numerators or the denominators the same so they can be compared.
- Example 1: Compare 2/3 with 4/5. Make the numerators the same, 4/6 & 4/5 and compare the denominators to the same whole. Fifths are more than sixths. Therefore, 4/5 > 4/6.
- Example 2: Compare 2/3 with 4/5. Make the denominators the same, 10/15 & 12/15 and compare numerators. Ten fifteenths are less than twelve fifteenths. Therefore, 12/15 > 10/15.
Eventually the idea that: The whole matters because fractions are part whole relationships, becomes a solid foundation for comparison.
Since fractions are counter intuitive, in several ways, it is helpful to frequently ask what is one (the unit) and to check their understanding of different values by asking how close the fractional numbers, they are working with, are to land mark numbers, (0, 1/2, 1, or other landmarks).
Addition and subtraction of fractions
Add and subtract fractions of equal parts:
Samples:
- A city block is about 1/12 of a mile. Chris walks three blocks to store, two blocks to the post office and five blocks back home. Home much of a mile did Chris walk? Represent it on a diagram and use it to explain.
- Chris comes to supper and finds that there are three pieces of a pizza, that was cut into four equal parts, left. If Chris takes two, how much of the pizza did Chris take and how much was left? (Both right with little hesitation super, both right or close to being right close, one wrong by a lot or both wrong not yet.
- Use of fractions in real life: Give me three ways you use fractions in your life? Without hesitation super, with hesitation and much thinking close, not able to not yet.
Suggestions for the introduction of addition and subraction of fractional numbers.
- Have students represent problems in multiple ways: concrete objects, models, pictures, diagrams, words (written and oral), act out, symbols.
- Start with concrete or visual representations.
- Introduce problems with real life stories.
- Start with problems that have common denominators.
- Create and give problems that include all the different addition and subtraction syntax (Join, separate, part-part-whole, compare or equalize.) Example: Join, with missing end or result unknown. Sandra ate 1/4 of a pie and Jimmy ate 1/4. How much was eaten all together?
- Include problems with mixed numbers along with problems that have common denominators.
- Move to problems with different denominators by doing problems similar to using measuring cups and pour 1/2 cup colored water into a measuring cup with a 1/4 cup oil and ask how much together. Discuss with models, pictures... and use problems from all groups of the different types of addition and subtraction.
- Introduce multiples and ratio table for students to use to find common multiples.
- Introduce mixed problems that have numbers and fractions with common and uncommon denominators.
Equivalent fractions
Use concrete, diagrams, and number lines to represent fractional values for learners to convince themselves fractional values relationships.
Algorithms for learners to develop:
Use multiples of one (2/2, 3/3, 4/4, ...) to divide or multiply to see if numbers are equivalent. Remember one time anything is the anything.
- Is 1/2 equivalent to 2/4, check by multiplying by one (2/2)
- 1/2 * 2/2 = 2/4;
- Or Is 1/2 equivalent to 2/4, check by dividing by one (2/2)
- 2/4 / 2/2 = 1/2;
Invert one fraction, multiple, & reduce. Can check to see if fractions are equivalent by knowing:
if a/b is equal to c/d, (equivalent fractions), then
(a*d)/b = c?
- Is 1/2 equivalent to 2/4, check
- (1 * 4)/ 2
- 4 / 2 equals 2,
- ∴ 2 = 2 & 1/2 is equivalent to 2/4
- Is 3/5 equivalent to 6/10,
- (3 * 10)/ 5
- 30 / 5 is 6 ∴ yes
Multiplication & division of fractions
Learners operate on fractional numbers with the same strategies as those used with different types of multiplication and division of whole numbers.
As learners become familiar with different ways multiplication and division operate to describe actions and compare numbers they are discovering how numbers are related with these operations. Different models can be used to illustrate and better develop these relationships when solving problem, for example: Cuisenaire models to develop four different types of multiplication of fractions.
Sample problem
A group of six people have five candy bars and want to share them equally. How much would each person get?
- A ratio of candy bars to children. Cut each candy bar into six pieces and pass them out to five people (distribute, partition, divide). Each person gets five pieces or 5 x 1/6 or 5/6.
- Partitive take five candy bars and cut three in half. If each person takes half there will be two pieces left. Take the two pieces and cut each into thirds. So each person gets 1/2 + 1/3 or 5/6.
Sample problem
I used 2/3 of a can of paint to cover 1/2 of the porch floor. How much paint will be needed for the whole floor?
- It is a ratio of 2/3 can to 1/2 floor. It is hard to see that it is partitive (distribute, partition, divide) since there is only part of a group (the floor).
Partitive
Three fourths, or three divided among or partitioned into four groups. (3/4 = 3/4). The equation seems like its saying the same thing so let's make it more concrete. Three sandwiches shared with four people. Each person gets 3/4 of a sandwich.
Three dollars shared with four people. Each person gets three quarters or 75 cents.
Review with whole numbers.
Partitive is thought of as division where a set is put into a certain number of groups.
For example 24 cookies are to be wrapped and put into lunch sacks for a team of eight. How many cookies can be wrapped for each player? (24 / 8 = 3) or (24 / ? = 8)
Or if a set a is put into b groups, it results in c number in each group.
c, is the quotient of a and b. (a / b = c ).
(Quotient is the answer to a division problem)
Quotitive and Measurement
If divison is introduced as fair sharing it is more likely seen as division and division with multiplication when 3/4 is understood as 3 * 1/4.
- A pie is cut into four equal pieces. One piece or 1/4 of the pie is removed. There are three equal pieces of one-four left. Three pieces are three times one piece, 3/4 = 3 * 1/4.
Quotative
Three fourths, or three out of four parts of the same one whole are shaded. This can be thought of as both multiplication and division. One whole divided into four parts with one-fourth shaded three times. Three-fourths put into one group.
Review with whole numbers.
Quotitive is thought of division where a set is put into groups.
For example 12 sandwiches are packaged 3 sandwiches to a bag, resulting in 4 bags.
Or Set a is put into groups the size of b, it results in a certain number of groups, c of size b being formed.
c, is the quotient of a and b. (a / b = c )
Measurement
When fractions are experienced as measurement/quotitive (shaded parts of a whole) the idea of division and multiplication can be lost.
Review with whole numbers.
Measurement is thought of division where a value or set is used as a unit of measure to measure another group.
If you want teams of five, and you have 20 kids, then how many teams will be needed? Or where set a is measured by the size of b, it results in a certain number of groups, c of size b.
c, is the quotient of a and b. (a / b = c )
Sample problems
3 1/3 / 1/2 = 6 2/3
Solution 1: Quotitive
This procedure is easy to memorize. However, it is much harder to model and explain how it works.
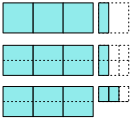 Divide 3 1/3
into groups of 1/2. How many groups?
Divide 3 1/3
into groups of 1/2. How many groups? - Three whole in half to make 6,
- The 1/3 is less than 1/2.
- So the answer is between 6 and 7.
- How do we find how much 1/3 is of 1/2?
- Draw a unit of one, divide it into thirds and mark 1/3 and 2/3.
- Then divide the same unit of one in half and mark 1/2.
- Notice that the 1/2 of the whole divides the middle third in half. Which tells us that piece is 1/3 of the 1/2 of the whole. This gets tricky so make sure you argree with it because you are going to need to use it soon.
This next part is the tricky part. We want to know how much of the 1/2 of the whole does the 1/3 of the whole represent? Well we just saw what 1/3 of 1/2 of the whole was so the 1/3 of the whole is twice it or 2/3.
- Therefore, 3 1/3 divided into halves will result in 6 2/3 halves.
- Another way of thinking about it is the thirds of 1/2 are 1/6 of one whole. Therefore, 2/6 of one = 1/3 but the 2/6 of one is 2/3 of the 1/2. This is fairly confusing, but is easier seen with diagrams.
Solution 2: Measurement
Or how many 1/2 pieces are in 3 1/3? This way takes a 1/2 piece and measures the 3 1/3. Again pretty easy for the 3 (six pieces of 1/2). But when the 1/2 is placed beside the left over 1/3 it becomes harder to see. However, a picture as described above should show that the 1/2 would measure 2/3 of the 1/2.
Solve this one both ways:
3 1/3 / 1/3 (=10)
Sample problem
2 2/3 / 1/4
- Ask, how many fourths in two two-thirds? (10).
- Can measure with 1/4. Four fourths in each one. For a total of 8., but how many fourths in two-thirds?
Solve with decimals
- 2/3 = .66 2/3, and .66 2/3 = .25 + .25 + .16 2/3, and 2/3 = 1/4 +1/4 + 1/6, because .16 2/3 is 2/3 of .25, because .08 1/3 + .08 1/3 + .08 1/3 = .25,
- But what is it of one? (.16 2/3) / 1 or (16 2/3) / 100 = 1/6, or how many 1/4 in 1/6 is the same as 1/6 / 1/4 = 2/3. Or 1/4 (4) + 1/4 (4) + 1/6 (4) = 1 + 1 + 2/3.
The answer (2 2/3) is in relation to 1/4 of an inch (first whole to consider), but there is also the inch (second whole to consider).
Another way to think of it is 2/3 / 1/4, find a common multiple /denominator of three and four and get, 8/12 / 3/12, then ask how many 3/12 (1/4) in 8/12 (2/3), 3/12 + 3/12 + 2/12, these three numbers represent the one whole to consider 2/3 put into 2 piles of 1/4 (3/12) and a leftover pile 2/12, To find the value in relationship to the second whole (one) we multiply all three by 4.
4 * 3/12 + 4 * 3/12 + 4* 2/12, and get 12/12 + 12/12 + 8/12, that is 2 2/3.
Decimals and percent
Decimals, percentages, fractions, and whole numbers have equivalent values, which can be used interchangeably.
Decimals are fractional base-ten equivalents represented by place value in our number system. In our base ten number system understanding of place value is necessary to develop understanding values of all numbers and their operations.
Percents are relationships based on a one-hundredth part of a whole, which are represented as fractions and decimals.
Review
- In addition and subtraction of fractions there is one whole that needs to be considered.
- Distributive and quotative division models each bring different ideas.
- Multiplication of decimals
Fraction to decimal to percent connections
Develop connections like:
- 1/2, .5, .50, 50%;
- 1/10, .1, .10, 10%,;
- 1/4, .25, 25%;
- 1/5, 2/10, .2, .20, 20%
Instructional Sequence for Addition and Subtraction Operations of Decimals
Remember, number value is the foundation to understand operations. Without a good understanding of number values for whole numbers, place value, fractions, land decimals, that are to be operated on with mathematical operations, and an understanding of a predicted result of the operation, it is not surprising learners are not aware of accuracy or inaccuracy of their result. They must be able to do all of this inorder to estimate and determine a reasonable answer.
To help learners develop their understanding it is helpful to focus learners on connecting concepts and ideas from whole numbers and their operations to decimal numbers and their operations
- Digits of numbers must be added according to their place values.
- Digits of numbers must be subtracted according to their place values.
- Decimals are another way of writing fractions
- Base ten is infinite in both directions
- Decimal point represents and when saying, reading, and writing decimal numbers.
- Decimal point locates the units position.
- Think of the decimal point as a smiley face.☺☺
Sequence of concepts and ideas
- Whole number place value is connected to decimal number place value
- Role of the decimal point
- Base ten infinitely large and small
- Connect fractions to decimals, decimals are another way of writing fractions - base ten fractions
- Explore rational numbers with models
- Use friendly numbers (tenths, hundredths, thousandths and percent) for addition and subtraction
- Include numbers greater than and less than one
- Use friendly numbers (tenths, .25, .5, .50, .75) for multiplication. Invent whole numbers times tenths are tenths, whole numbers times hundredths are hundredths, tenths times tenths are hundredths.
- Use friendly numbers for division - There are 12 people and 10 subs. How much subs do each person get? do multiple ways.
- Generalize a rule for multiplication and division based on base ten.
Activity sequence
- Review whole number place value - say, write, read, numbers activity
- Role of the decimal point - smiley face decimal point
- Base ten numbers can be infinitely large and small - use strips and squares (10 x 10), 100 chartand other models to show different representations for decimal numbers.
- Connect fractions to decimals and decimals to fractions. Decimals are another way of writing fractions - base ten fractions
- Use friendly numbers (tenths, hundredths, thousandths and percent) for addition and subtraction. Include numbers greater than and less than one. Use strips and squares (10 x 10) models to model problems.
- Use money to explore decimal numbers and the operations of addition and subtraction.
- Use a meter stick to explore decimal numbers and the operations of addition and subtraction.
- Use circular disks to explore decimal numbers and the operations of addition and subtraction.
- Use friendly numbers (tenths, .25, .5, .50, .75) for multiplication. Invent whole numbers times tenths are tenths, whole numbers times hundredths are hundredths, tenths times tenths are hundredths. Include numbers greater than and less than one.
- Use friendly numbers for division - There are 12 people and 10 subs. How much subs do each person get? do multiple ways. Include numbers greater than and less than one.
- Use money to explore decimal numbers and the operations of multiplication and division.
- Use a meter stick to explore decimal numbers and the operations of multiplication and division.
- Use circular disks to explore decimal numbers and the operations of multiplication and division.
- Generalize a rule for multiplication and division based on base ten. Include numbers greater than and less than one.
- Real world problems with whole, fraction, and decimal numbers to apply all above.
Strategies for solving addition & subtraction of fractions
Lines
Sample
- 1/4 + 1/5
- Pretend you are going on a trip.
- What would be a good distance to use?
- 100 blocks? miles?
- Draw a line.
- Put 0 and 100 at the ends. Why 100? I thought: 1/4 of 100 is 25 and 1/5 of 100 is 20.
- Draw another line parallel to it.
- Put 0 and 1 at the ends.
- You now have a: double number line (with fractions and whole numbers).
- Mark 25 and 20 on the 100 number line and extend the lines to the other number line.
- Fractional values are 25/100 + 20/100; 45/100
- Or 1/4 + 1/5;
- Or ... Could have started with 20 blocks, 20 miles, 20 km.
- Make double number line
- Put the values on the lines
- 1/4 & 5
- 1/5 & 4
- 9/20
- Or ... What about 10?
- 2.5 is 1/4 because 5 is 1/2
- 2 is 1/5 because 2 * 5; 10
- ∴ 2.5 / 10 + 2 / 10;
- 4.5 / 10
- Mark all of these on one line or make a stacked number line.
Try:
2/4 + 1/5
Do with 100, 10, 20, ...
Using time and the clock for problems
Problems
My son suggested that a good way to exercise is to jog for 1/3 of an hour and walk for 1/4 of an hour. How much time is that altogether?
Or I could walk for 1/3 hour, jog 1/2 hour, and walk for 1/3 hour. How much time?
Or 1/4, 1/3, 1/4, ...
Write as reduced fraction and fraction with denominator of 60, could make ratio table.
Clock chart or pie chart.
Sample problem
Time on a clock. Mark a clock with fourths, thirds, fifths, sixths, and tenths.
- Add different fractions. 1/3 + 1/4 as how many minutes plus how many minutes?
- 1/3 (20 minutes) + 1/4 (15 minutes);
- (20 minutes + 15 minutes);
- (35 minutes);
- 7/12
- Or 1 1/4 - 2/3;
- Start with 1:15 or 75 minutes
- go back 40 minutes;
- arrive at 35;
- or 7/12
Again 1/2 + 1/6 = 2/3, 30/60 + 10/60 = 40/60 = 4/6 ...
Would the clock be useful for sevenths?
Make a list of fractions for which the clock would be useful.
Strategies for solving multiplication & division of fractions
Visualization
As in division of fractions, multiplication or fractions requires two wholes be consider for each problem: A relation of a relation.
Example
1/6 of 1/2, (1/12)
- Asks what is 1/6 of one-half. Divide 1/2 into sixths and each piece is 1/12 of a starting unit for which 1/2 was made.
- Need to consider a (one) whole to use to represent one-half
- Then, need to consider the 1/2 as a (one) whole to find 1/6
- Then finally need to consider what part the 1/6 of the half is of one whole; 1/6 This can be modeled and visualized with Cuisenaire rods, area models (arrays & rectangles) and other models used with whole number multiplication and division
Measurement quotitive division
Sample problem
How many bags of cookies can be make with 12 cookies and three bags?
- Shade three of four parts and label. Starting with a quotative model is not the place to start. It does not emphasize the whole and the relationship to the whole is missed.
Sample problem
John is baking a cake and only has a 1/2-cup measuring tool. The recipe calls for 2/3 of a cup of flour. How many times should he fill the 1/2-cup?
- This is quotative, not just because it involves measurement. It asks how many 1/2 cups fit in 2/3rds a cup. This is more difficult for children to understand and is usually done by making common denominators.
Eventually students should link the two ideas and see they are the same. Five bars divided by six kids is 5 x 1/6; The 5/6 mark on a strip is also 5 x 1/6. That shows how multiplication and division are related. Fractions are multiplication and division.
Algorithms vs. number sense
6/16 * 8/18 (I would switch the numbers and reduce (1/2 * 1/3 = 1/6.)
Chinese teachers would decompose the numbers to expanded notation and multiply the parts like 6 * 8 * 1/16 * 1/18. American teachers teach the algorithm (multiply top numbers and bottom numbers) without conceptual understanding and treat errors as procedural errors of digit manipulation.
Use arrays to multiply. 3/5 * 5/6 Show in arrays three ways. 3x5 and 5x3 showing 3 * 1/5 with 5 * 1/6 shaded to show four different parts of problem and whole. Then switch the directions of the two numbers and repeat. Then show the answer (15) in relation to the whole (30).
Write problems as 2 * 3 * 1/3 * 1/5 for 2/3 * 3/5 ...
Use factors, commutative, & distributive property
Sample
Can use fact families:
- 3 * 8 = 24
- 8 * 3 = 24
- 24 / 8 = 3
- 24 / 3 = 8
To create different problems:
Represent with an array (3 * 8)
- Think of three dots in a row and eight rows. Can ask:
- What is 1/8, 1/3, 3/24, 24/8 ...
- What is 1/4, 1/6,
- What i 1/2?
- How represent 6 * 4, 8 * 3, ...
- What is 3/8?
- It's like the three is one and the eight is the whole (8 groups of 3 made from the 24).
- It's really cool how multiplication and division helps us with fractions. (It's the relationship.)
Students who have difficulty visualizing the different ways to arrange the arrays can be supported by rearranging the numbers. (3 x 8) to (4 x 6) (2 x 12)
May also try placing four 8-dot dominoes in a rectangular pattern for the problem (3 * 8) and using the six side of four dice for the problem (6 * 4)
Could also use pennies to cluster in any rectangular pattern.
Problem: communtative property
3 1/2 * 14;
- Think of the problem as (3 + 1/2) * 14; then
- (3 * 14) + (1/2 * 14);
- 42 + 7;
- 49
Sample: sample factors, commutative, & distributative properties
- 4 1/2 * 50; use factors and commutative property
- double by 2 and divide by 2
- 9 * 25; 225
- 4 1/2 * 50; use factor and distributive property
- (4 * 50) + (1/2 * 50)
- 200 + 25; 225
- 4 1/2 * 50; use factor and distributive property
- (5 * 50) - (1/2 * 50)
- 250 - 25; 225
Sample: sample factors, commutative, & distributative properties
- 2 1/4 * 120; use factors and commutative property
- double by 2 and divide by 2
- 4 1/2 * 60
- 4 * 60 + 1/2 * 60
- 240 + 30; 270
Sample: sample factors, commutative, & distributative properties
- 15 1/2 * 36; use factor of ten and distributive property
- (10 + 5 + 1/2) * 36
- (10 * 36) + (5 * 36) + (1/2 * 36); multiply 10 * 36, divide & multiply by 10, take 1/2
- 360 + (1/2 * 360) + 18
- 360 + 180 + 18
- 460 + 88
- 460 + 40 + 48; 548
Sample: sample factors, commutative, & distributative properties
- 15 1/2 * 4 1/2
- (15 * 4) + (15 * 1/2) + (1/2 * 4) + (1/2 * 1/2); use double & halves, halves, halves, halves
- (30 * 2) + (7 1/2) + (2) + (1/4)
- 15 + 7 1/2 + 2 + 1/4; commutative property
- 15 + 7 + 2 + 1/2 + 1/4
- 24 + 3/4; 24 3/4
Sample: doubles & halves
- 4 1/2 * 50; rewrite
- (4 + 1/2) * 50; distributive property
- (4 * 50) + 1/2 * 50; halve & double
- (2 * 100) + (25); again
- (1 * 200) + 25; 225
or double & halfto get rid of fraction
- double 4 1/2 and half 50
- 9 * 25
Open arrays
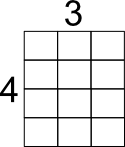 Arrays may be too easily constructed procedurally, that lerners do not
see them conceptual. A person really has to think to see the fractional
relationship on an array within an array.
Arrays may be too easily constructed procedurally, that lerners do not
see them conceptual. A person really has to think to see the fractional
relationship on an array within an array.
1/3 * 1/4 (array 3 x 4)
2/3 * 1/4 (use same array, is it twice the other? Why?)
2/3 * 3/4 (How does this compare with the two preceding?)
4/3 * 3/2 Make a 3 x 4 array 2 x 3 would be the whole ...
Might try 1/2 of 4/3 first, then 2/2 * 4/3, then 3/2 * 4/3
Then do these and transition to swapping numerators and denominators
1/5 * 1/7
3/5 * 4/7
Swapping numerators and denominators
4/5 * 3/7
Or 4 * 3 * 1/5 * 1/7
If only an array is used students will notice that the inside array and the outside array are the same, only rotated 90 degrees, and see that multiplication is commutative (doesn't matter if multiply 1/2 * 2/3 or 2/2 * 2/3) but not understand multiplication of fractions conceptually.
3/8 * 4/9
5/6 * 3/5
4/5 * 5/8
Use to find when swapping is a useful strategy.
Getting rid of a fraction
Concrete models for multiplication of fractions with Cuisenaire rods
Strategies for Multiplication of fractions
- 3 1/2 * 18; double (3 1/2) to get rid of the fraction and halve (18) to maintain equality);
- 7 * 9; 63
- 3 1/4 * 28; multiply by four to get rid of the fraction 3 1/4) and divide by four (28) to maintain equality
- 13 * 7;
- 70 + 21; 91
- 3 1/2 * 14; (multiply by 2 and divide by 2) (3 1/2 * 2) * (14 / 2); 7 * 7 = 49.
- 2 1/4 * 16 (multiply and divide by 4) 9 * 4 = 36
- 3 1/5 * 45 (multiply and divide by 5) = 16 * 9 ; 8 * 18; 4 * 36; 2 * 72; 144
- 3 1/5 * 50
Division
Remember this earlier problem? See quotative and measurement above.
- 3 1/3 / 1/2; multiply both factors by two or double each factor
- 6 2/3 / 2/2
- 6 2/3 / 1
- 6 2/3
- 3 1/2 * 1/2
- 3 1/5 * 1/5
- 3 1/5 * 1/5
- 2 1/4 * 1/2
Developing strategies for computation with decimals
Use strategies, for whole numbers
Use strategies for whole numbers, solve the problem as if the numbers are whole numbers, use the place value of the decimal numbers to determine the placement of the decimal. Example: if adding and subtracting the decimal point belongs between the ones and tenths. Placement of the decimal point for multiplication and division can be resolved by considering multiples of ten (tenths * a whole number is tenths; tenths * tenths is humdredths;
Get rid of a decimal
Multiplication
Sample
- .8 * 30 multiply and divide by 10 to get rid of the decimal
- (.8 * 10) * (30 / 10)
- 8 x 3: 24
- Or ignore think 8 * 30 is 240 and since it is tenths times whole numbers, the answer is tenths; 240 / 10 or 24.0
Friendly numbers
Sample
- 71.87 + 28.2; compensate: subtract .2 and add .2 (move .2 from 28.2 to 71.87)
- 72.07 + 28;
- 100.07
or - 71.87 + 28.2; compensate: subtract .8 and add .8
- 71.07 + 29;
- 100.07
10.5 + 21.5
27. 2 + 33.8
23.6 + 34.4
46.3 + 32.75
Sample problem
Chris told Pat that s/he was .8 of the way to their goal of each saving a certain amount of money Pat said that s/he had only .5 of what Chris had. What part of their goal did Pat have?
- Chris has .8 of their goal.
- Pat has .5 (1/2) of what Chris has (.8).
- ∴Pat has 1/2 of .8;
- .4
Arrays make a ten by ten grid and shade .4 of .8. Can also show that 1/2 * 4/5 is the same by making a two by ten array.
Think money
Sample
- .20 * 9; think of .20 as 20 cents
- use distributive property
- .20 * 5 + .20 * 4
- 1.00 + .80; 1.80
or - .20 * 9 round to 10
- .20 * 10
- 2.00 - .20; 1.80
.20 * 7
.20 * 12
.20 * 16
Think quarters, four quarters = $1.00
4 * .25
8 * .25
.25 * 9
16 * .25
How many students would know that a 4 x 4 array of quarters is 4 dollars?
Change fractions and decimals
Sample
- 75 * 80; think of 75 as .75, 75/100, or 3/4
- 3/4 * 80 * 100
- 60; because 75 was treated as 75/100 or divided by 100, need to multiply 100
- 60 * 100;
- 6 000
1/4 * 80
.25 * 80
25 * 80
1/2 * 60
.5 * 60
.50 * 60
.50 * .60
Getting rid of a percent
Sample
Chris wants to buy a leather coat for $350. Mom said she would help, but Chris would have to pay 80%. How much would Chris have to pay?
- 80% of $350.00; think decimal (.80 or .8)
- .8 * 350; multiply and divide by 10
- 8 * 35; divide by 2 and multiply by 2
- 4 * 70; do it again
- 2 * 140; one last time
- 280
or use fractions - 80% of $350.00; think .8 or 4/5
- 4/5 * 350; multiply and divide by 5
- 4 * 70; 280
or - 80% of $350.00; think .8 or 4/5
- 4/5 * 350;
- 4 * (1/5 * 350);
- 4 * 70; 280
Liam wants to buy a coat for $150. Mom says it is more than what she would pay for her coat, but if Liam wants to use his savings, she will pay 50%. How much would Liam have to pay?
Emma wants to buy a puzzle for $14. Mom said she would pay 50% if Emma would ... How much would Emma have to pay?
Write one of your own.
Practice problems
Identify the equivalent decimal and percent for the following.
- 1/2
- 1/4
- 3/4
- 1/3
- 2/5
- 4/5
Write the problems two other ways and find the product. Fraction, decimal, percent
Sample: (1/2 * 66; 33) (.33 * 66; 33) (50% of 66; 33)
- 1/4 * 80
- . 75 * 80
- .60 * 100
- 1/2 * 60
- .5 * 60
- 50% of 60
Use an array to show 48 / 12 and answer these questions.
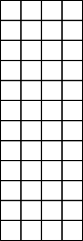
Hint: Use an array of 12 rows and 4 columns.
Describe the relationship:
- If the array is one, then a row is
- If the array is one, then a column is
- If the array is one, then a cell is
- If the array is one, then two rows are
- If the array is one, then two columns are
- If the array is two, then a row is
- If the array is two, then a column is
- If the array is four, then a row is
- If the array is four, then a column is
- One row is what part of a column?
- One column is what part of a row?
- If a row is 4/12, then what is the array?
Try to use different strategies to solve these:
1/3 * 1/4
2/3 * 1/4
2/3 * 3/4
1/5 * 1/7
3/5 * 4/7
4/5 * 3/7
3/8 * 4/9
5/6 * 3/5
4/5 * 5/8
6 * 10
12 * 5
24 * 2 1/2
8 * 30
16 * 15
32 * 7 1/2
64 * 3 3/4
18 * 5 1/2
3 1/2 * 14
9 * 11
4 1/2 * 22
14 * 3 1/2
4 / 1/2
8 / 1
16 / 1/4
32 / 1/2
64 / 1
5 1/2 / 1/3
16 1/2 / 1
2 1/2 / 1/5