Fractional number values development, instructional ideas, sample activities, and assessment to represent fractions and decimals
Page Overview:
- Fractional models
- Equivalence
- Comparing fractions
- Sample model worksheets
- Fractional parts of a shape
- Cuisinaire rods
- Pattern blocks
- Fractional parts of a group (set)
- Fractional parts of a circle
- Fraction wheel
- Fractional parts of a square challenge
- Number line with12 spaces
- Number line with 36 spaces
- Multiple number lines for an enlarged one inch ruler
- Number lines for decimal equivalents
- Fractional strips
- Hundred chart
- Four 10 cm hundred charts
This page includes information on tasks to facilitate the development of fractions: fractions as equal parts of a whole, fractions as equal subset of a group, and equivalent fractions to hundredths. The use of fraction circles, fraction disks, paper folding, area models, measurement models, and number lines to represent fractional values.
Also see:
number lines background information, and Fraction concepts & misconceptions
Young students can explore fractions as equal parts of a whole visually before they conserve area if the areas are identical in shape as the area of the whole. For example: half of a square in the shape of a rectangle or triangle which is half of a square as the whole or unit.
Activities where students explore different shapes and discuss which are identical, which are not, and then which parts of other shapes can fit together to make the original shape, help them conceptualize concepts of fractional values. Showing how two identical shapes can fit into a larger shape. For example: a square can be made with identical rectangles (each 1/2 of the square), two identical triangles (each 1/2 of the square). Pattern blocks can be manipulated to represent this as well as cutting paper, or folding paper to verify equal sizes. Those that are and can be used to complete a larger shape entirely can be identified as fractional parts (1/2, 1/3, & 1/4).
Similar strategies can be used with older students as they develop spatial abilities to rotate and flip shapes and objects to identify fractional parts in more complicated representations.
See also operations of fractions, decimals, percents, ...
Fraction models
Area model
Fraction as equal parts of a whole.
Give fractional strips and ask to fold them into different fractional values (1/2 & 1/3). Verify with folding.
Give fraction circles and ask to fold or color them into different fractional values (1/2, 1/4, 3/4, 1/3, 2/3). Verify with folding or counting equal fractional parts.
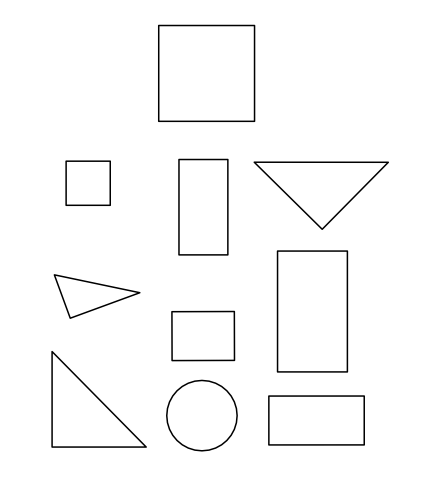
Challenge with examples of fractional parts of shapes to identify specific fractional parts (1/2, ...). A whole shape and parts of the shape of different sizes. Verify by folding or placing fractional parts on whole.
- Ask. Describe which shape is one-half of the square. If students don't comment on the portion size of each piece, ask them questions about the size of each part. Have them verify their answers by folding the square or strips in halves.
Worksheet samples:
- Fractional parts of a shape
- Cuisinaire rods
- Pattern blocks
- Fractional parts of a group (set)
- Fractional parts of a circle
- Fraction wheel
- Fractional parts of a square challenge
- Number line with12 spaces
- Number line with 36 spaces
- Multiple number lines for an enlarged one inch ruler
- Number lines for decimal equivalents
- Fractional strips
- Hundred chart
- Four 10 cm hundred charts
Area & volume models
Fraction values with Pattern Blocks & Cuisenaire rods (area? & volume models)
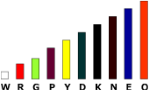
Give students a variety of pattern blocks or Cuisenaire rods (see chart below) and ask them to show 1/2, 1/3, 2/3, 3/4, and 1 1/2 .Have them verify their answers by arranging equal rods or blocks to match the unit block or rod. Scoring guide or rubric
Worksheet samples:
If students can't complete
the task on their own, prompt them by giving them a block to use as the
value of one and ask if they can show the fractional part of it. (1/2, 1/3,
2/3, 3/4, and 1 1/2) Scoring guide or
rubric 
| Fraction | Rods |
|---|---|
| 1/2 | Red and white, Red and purple, Yellow and orange, Light green and dark green, |
| 1/3 | Light green and blue, Or white and light green, Or red and dark green |
| 2/3 | Light green and blue, Or white and light green, Or red and dark green, |
| 1 and 1/2 | Red and white, Red and purple, Yellow and orange, Light green and dark green, |

Fractions with Pattern blocks (area? & volume models)
Give students an assortment of Pattern blocks and ask them to show you 1/2, 1/3, 2/3, 3/4, 1 1/2. Have them verify their answers by arranging equal rods or blocks to match the unit block or rod.
| Fraction | Pattern Blocks |
|---|---|
| 1/2 | Yellow hexagon and red trapezoid Or blue parallelogram and red trapezoid |
| 1/3 | Red trapezoid and green triangles, Or yellow hexagon and blue parallelogram |
| 2/3 | Red trapezoid and green triangles, Or yellow hexagon and blue parallelogram |
| 1 and 1/2 | Yellow hexagon and red trapezoid, Or blue parallelogram and red trapezoid |
Measurement model
Fractions with length or measurement models:
- Give students a ruler and ask them to show you 1/2, 3/4, and 3/8 of an inch. Have them verify their answers by counting the number of spaces in an inch, cm, or m for the unit (inch, foot, cm, m).
- If they can not then prompt them by showing them 1/8, 1/4, and 1/2, then ask them to show you 3/4, 3/8 and 1/2.
- Fractions on number lines
Worksheet samples:
- Fraction strips
- Number lines
- Rulers - locate fractional parts of an inch: 1/2, 1/4, 1/8, 1/16, 3/8, 2/4, 3/4 ...
- Rulers - locate fractional parts of a cm and m : 1/2, 1/5, 1/10, 2/4, 2/5, 2/10, 3/10, ...
Sub sets
Fractions as subsets of a group (set):
Give students collections of objects and ask them to show you 1/2, 1/3, 1/4, 1/5, 1/6, 2/4, 3/4, 3/6, 2/5, 3/10 ... Have them verify their answers by arranging equal subsets for the fractional number of subsets in the group.
If they can't prompt them by dividing the set into two groups and asking what is 1/2.
Five groups and ask what is 2/5.
Spread the set out and ask what is 3/10.
Worksheet sample:
Equivalent Fractions
Give students a fraction wheel and ask them to explain what different parts are equivalent. Have them verify their answers by showing the equal the fractional number of fractional parts of in the circle.
Ask. Can you show equivalent fractions.
If they can't prompt them by showing them that the inside circle is 1/4, then ask them if that helps them know what the middle section and outer section is. Then ask what that has to do with equivalent fractions.
Worksheets & samples:
- Multiple number lines to represent equivalent fractions
- Fraction wheels to show equivalent fractions
- Cuisenaire rods
- Pattern blocks
- Fraction strips
- Number lines
- Show students a ratio table and ask how it could be used to find equivalent fractions. Look at the first column looks like 1/2, then look at the relationship in the next columns.
- Use a sheet of dot paper with 3x7 array of 21 dots in a rectangle so 12 squares can be made. Ask if they could show 1/3, 2/6, and 4/12 and if they are related. If they can't suggest that they draw lines to make squares.
Comparing fractions
Comparing fractions as equal, greater, or less:
Ask students how they would arrange 1/2, 1/3, 1/4, and 2/3 in order and how they know they are right. Shaded values on equal sized fraction strips and number lines can be compared by lengths. Others by areas or volumes if the units are the same.
Worksheet sample:
Using one
Know what represents one and the different parts of a fraction (numerator & denominator).
Samples:
- Use any of the object or shapes to ask. Use these objects (collection of Cuisenaire rods (W, R, G, D, B, ... ) and show 1/3. What does the one (numerator) represent? What does the three (denominator) represent? What represents a whole?
- Next give them an object, that can represent 2/10, (red Cuisenaire rod if O (orange) is one) and say. If this (red rod) is 1/5, what is one (O).
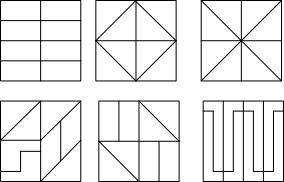
- Use a shape and have learners see how many ways they can divide it into fractional parts. Example: How many different ways can you divide a square into eights? Sample
Activity sheets
Fractional parts of a shape: Square and Parts
Find which shapes are 1/2 (one-half) of the top square.
Cuisenaire Rods for Fractional parts
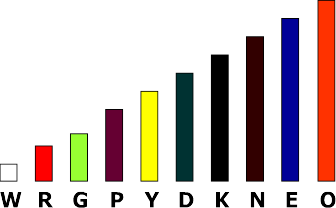
What fractional parts can you illustrate for the different rods?
Pattern blocks

What fractional parts can you illustrate for the pattern blocks?
Fractional parts of groups
What fractional parts are the different colors?
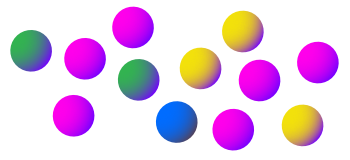
Green
Pink
Yellow
Blue
What is one?
Fractional parts of a circle
What fractional parts can you make in the circle?
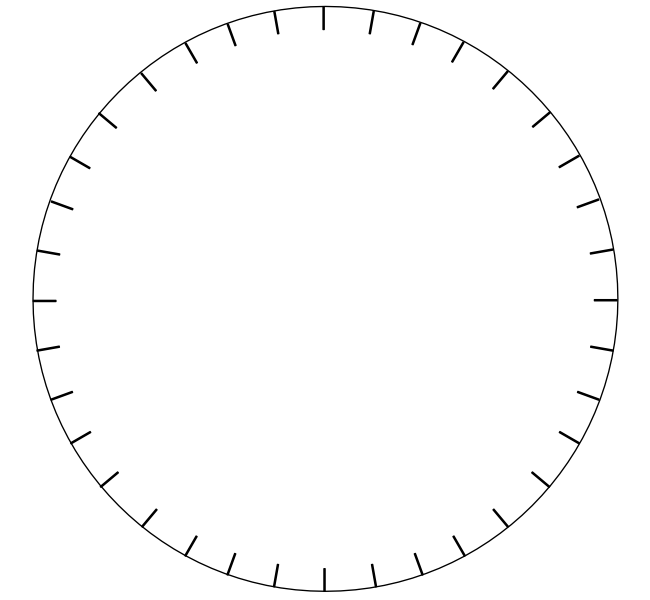
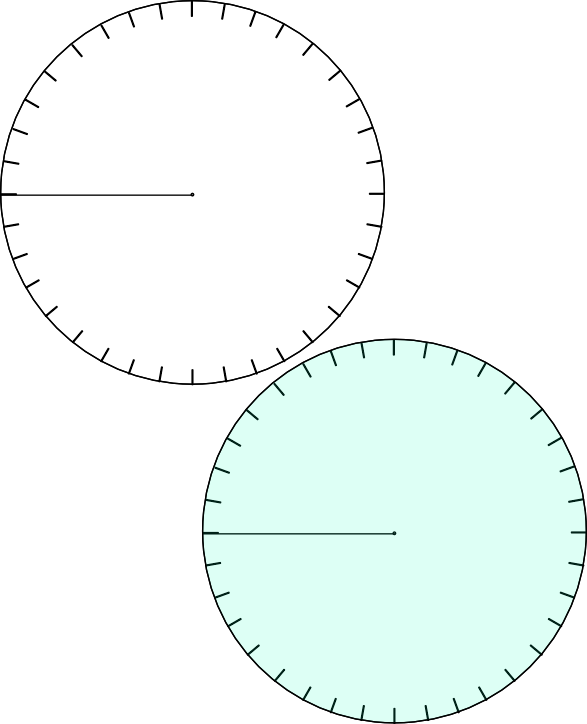
Fraction Wheel
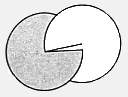 Cut out each disk. Cut along the radius line. Slide each disk inside the other. Rotate the wheels to show different fractional parts of a circle.
Cut out each disk. Cut along the radius line. Slide each disk inside the other. Rotate the wheels to show different fractional parts of a circle.
Fractional parts of a square challenge
What fractional parts do the different shapes in the square represent?

Number lines for fractional parts
Number line with 12 spaces
What fractional parts can you represent on the number line?
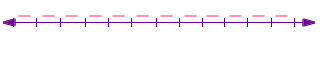
Number line with 36 spaces
What fractional parts can you represent on the number line?
![]()
One inch ruler for fractional parts
What equivalent fractional parts can you represent on the first inch of an enlarged ruler?

Number lines for decimal equivalents
What decimal parts can you represent on this enlarged centimeter or reduced meter?

Fraction strips: 10 & 20
What fractional parts can you represent with a strip?



What fractional parts can you represent on the strips if one strip is 1/2 or two strips =1?

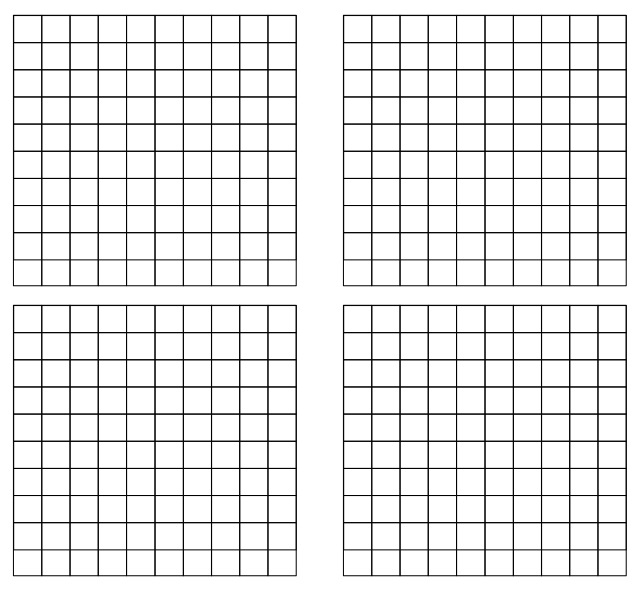
Hundred chart
What fractional parts can you represent on the square?

Hundred charts
Make fractional parts equivalent to 1ooths (.01).
Sample of different ways to divide a square into eights
Challenge. How many different ways can you divide a square into eights?