Development of Multiplication and Division
Understanding and Strategies
- Big ideas
- Developmental background information
- Representations of multiplication and division
- Types of division
- Strategies
- Visualize
- Iterate equal groups
- Multiples, factors, primes, composites
- Use Properties: distributive, commutative, associative
- Developing algorithms
- Sample Problems
Critics often target teachers and schools when they feel students do no know the basic facts and lack proficiency of multiplication and division algorithms.
They use emotional words like:
New math, fuzzy math, soft math, and claim it is dumbing down student's learning of mathematics.
However, mindless use of algorithms
is the real dumbing down.
Big ideas - concepts and generalization for multiplication and division
Multiplication and division are ways to describe how two (or more) values (of sets of objects) correspond and can be operated on to create another value that is equivalent to the initial values in the following ways:
Multiplication can be represented as:
- A correspondence of value between two (or more) sets of objects. Visualized concretely by young children like. Two crackers for each piece of cheese. Five players for each team. Solved procedurally with repeated addition. As children develop, they can recognize this correspondence can be
- A unit (unitized, simultaneously as a unit and a group) and iterated to find the product of factors.
- Measurement of like units combined for area, volume, comparisons, rates, and other measurements. A product that is something different than the factors (square feet is the product of linear feet, cubic cm...).
- Arrays, grids, matrices
- Combinations or Cartesian products
- Trees
- A product of a factor times a factor, as learners move toward formal operational.
- 4 (factor) * 3 (factor) = 12 (product)
Division can be represented as:
- measurements of how different values of objects correspond (are operated on) to create equal groups.
Example: An elderly person lives in a shoe and gives candy bars to the children who live there too. If there are 144 bars and one is given to each of the 22 kids who live there too, how many days will the bars last? Measure the total number of bars with 22 as the measure. - distributions or partitions of fair shares.
Example: An elderly person lives in a shoe and has 144 candy bars to give to the children who live there too. If there are 22 kids, how many bars will each child get? Partition fair shares to 22 kids. - a dividend divided by a divisor resulting in the quotient and sometimes a remainder
7 (dividend or something to divide) / 2 (divisor or number to divide) = 3 (quotient or result of division) sometimes with a remainder (1) as learners move toward formal operational.- Remainders can be dealt with four ways: round up, round down, divide equally, or toss away
More - concepts, misconception, & outcomes for multiplication, division, & their properties
Developmental of multiplication & division
Let’s begin by reviewing the mental operations necessary for logically thinking mathematical learners use to construct understanding multiplication and division and their properties. Mental operations such as: conservation, decentering, transforming, reversing, classification, inclusion, and of course logical mathematical thinking instead of transductive reasoning, which can be assessed with conservation tasks.
Let’s start with a multiplication problem.
Mom usually only allows me to have four cookies at a time. However, since I have two friends over, I think I may get her to give us five, if I ask in front of my friends. It doesn't work. She says nice try and hands me a stack of cookies and says, here are four for each of you. Go ...
How many cookies did mom give me? 12
![]()
This can be represented with groups: three groups of four and with the operation of multiplication as three times four; 3 * 4.

To understand what these values represent and how multiplication operates on them, a person must know how the arrangement of the numbers (values) are expressed with the operation. To do this a person must have constructed mental operations of conservation, decentering, transforming, reversing, hierarchical inclusion (for repeated addition or repeated subtraction, and iteration of equal groups). Fundamental Theory of Arithmetic (FTA) to understand how factors can be used in different strategies, half, double, tens, … so they don't memorize a procedure and not understand how it works.
That is, they must:
- Conserve numbers. Know the value of 12, cardinality of 12 objects, is constant no matter where or how the objects are placed.
- Decenter from inaccurate information. Like believing visual representations, that support the value of the objects, change as they are moved: stacked, spread out, grouped, cut into halves; to believing the observation is misleading and look to a more logical and accurate explanation for why the values don’t change.
- Transform the objects accurately as they move into groups, knowing they change physically, but the total value (cardinality) is conserved.
- Reverse the objects from ungrouped to grouped and back again or from group to group and back again to verify a transformation will not change them physically or their total cardinality as the objects are regrouped.
- Class inclusion. An object or set of objects can be included in more than one group at a time and hierarchical inclusion for operations. (sums and products have equivalent values of which can be created by operating on numbers with smaller values (5 = 0+5, 1+4, 2+3, 3+2, 4+1, 5+0) (12 = 1*12, 2*6, 3*4, 4*3, 6*2, 12*1))
- Stop transductive and egocentric thinking of anything that isn’t accurate and replace it with logical mathematical reasoning.
- See also development of children preK - second grade.
Learners who have not constructed these ideas well, will count the objects, put them into groups, count them again, move them out of groups, count them again and again to check what is happening. They may decenter from transductive reasoning and center on logical mathematical reasoning for accurate explanations. However, if they do, their conclusions will be fragile and need several experiences for them to gain confidence in their reasoning.
As they build their confidence in the operations by manipulating concrete objects or representations of objects in diagrams, they will discover validate conclusions. For example exploring the circles and stars game. Where they roll a die, draw circles to represent a group, roll a die, and draw stars in the circles to represent the number of stars in each group. Later, with enough experience, they can apply their ideas, less concretely, with numerals and labels.
One might think iterating groups would be sufficient to use as a model for multiplication and division. It is important and one of the most used models for many multiplication and division situations. However, the use of rectangle and array models can facilitate learners to move beyond multiplication as repeated addition to operating as multiplication.
Let's see how.
Take the cookie and friends example and represent it with a rectanglar array. The friends (groups) are represented by three rows, the cookies distributed equally to each person by the columns, with each cell representing a cookie.
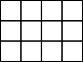
This is more than a linear represenation where a person corresponds to a group of cookies and their group of cookies corresponds to the number of cookies they get. Similarly for the the other two friends. This is represented by circling four cookies three times as in the diagram above.
To understand how a rectangle representation works, a learner must reason with the mental operations: conserve number, decenter, transform, reverse, stop egocentric thinking, recognize inclusion, and use logical mathematical reasoning. And additionally show how equal groups are related and each can be thought of as a group and units simultaneously (unitize).
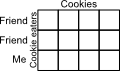
Let's review what is represented in the array:
- Rows represent: one person (cookie eater), that person's group of cookies, and the four cookies in that group.
- The columns represent an equal group of cookies that will be part of the total group each person will receive.
- Over all the array represents all the cookies given to the students with one cookie in each cell.
This representation helps facilitate the idea of unitizing, which is important for multiplication, division, place value, fractions, decimals, and all mathematical ideas where values and statements have multiple relationships.
Each cookie in the array is located in a cell. Its position shows how it corresponds to a person, a person's group of cookies, and a group it was distributed with (one group to each person or three groups or four cookies)
Let’s review:
- Each person has a group of 4 cookies; 1 times 4 for three people; one cookie in each group for each person, four times. 12 cookies distributed to 3 people; 4 cookies per person.
- Four groups of three cookies are distributed to each person; 4 times three coookies; 12 cookies
- 12 objects can be arranged into three groups of four; 12 cookies divided into three groups; is 4 cookies
- Four groups of three cookies were distributed to three people; 12 cookies distributed to 3 people; 4 cookies per person.
- Twelve cookies can be distributed into equal groups of three and four.
- Any I missed?
To be able to understand these ideas learners must stop egocentric thinking, recognize inclusion, use logical mathematical reasoning to transform objects into different groups, reverse them back to the original group, and verify cardinality is conserved when transformed and reversed from group to group.
Young learners will not understand all these ideas, however, each time they experience them they may increase their understanding, which will help them develop little by little and as they do, providing tools to use to understand other mathematical ideas: place value, fractions, decimals, exponents, algebra, and more.
Rectangular arrays and other representations help learners construct these relationships if probing questions are asked to lead them to see these relationships and give them time to slow down and verify each step of an operation to convince themselves which actions are logical and provide consistent and accurate results.
Similarly logical mathematical thinking, transformation, reversibility, and conservation of cardinality are necessary to conceptualize the commutative, associative, and distributive properties. As you continue to explore consider how these basic mental operations are prerequisites for understanding the ways of multiplication and division operations.
Developing multiplication & division

Initially learners visualize multiplication as a correspondence of objects [objects (fingers) to object (hand] and operate on them with repeated addition. This can be seen in their use of concrete objects and diagrams they make of equal groups and repeated addition to operate on them.
Young children will solve a problem (4 cookies to 3 children) by counting 4 objects or drawing 4 cookies into three groups with a one to one correspondence. Then count all the objects in each group again with a one by one count to find the total number of objects, (12) in all the groups combined. They do not unitize (see each group as a unit and a group).
- Three children are each given four cookies. How many cookies did all the children get? 12
- Count out or draw four cookies and place them one at a time into three groups
- (1, 2, 3, 4); (1, 2, 3, 4); (1, 2, 3, 4); (1, 2, 3, 4), then
- count all the cookies represented one by one (1,2,3,4,5,6,7,8,9,10,11,12).
When representing multiplication for young children (2 * 3) use two groups with three objects or draw two groups with three objects. Be consistent. Always read as two groups of three. Always make the first number the groups and the second the number of objects in each group.
Good activity to do is the Circles and Stars Game:
It is played with a die, pencil, and paper. Start by rolling a die. The first roll is used to draw as many circles as dots on the die (groups). Then roll the die a second time and draw that many stars in each circle (objects in a group).Then write an equation to represent the rolls, stars, and number of circles. Learners can chart all possibilities on a class chart and talk about possible combinations for probability (lesson plan for dice & probability), patterns, factors, and multiples.
As learners develop they will eventually use a group or factor to repesent its value and its correspondance as a measure to iterate. This will represent or correspond as the number of iterations, to use to find the total number of objects needed to solve a multiplication or division problem.
For example: to find, how many total objects are needed to share equal amounts of a known quantity with a known number of groups. The number of objects that represent the group can be iterated, or unitized, which makes multiplication different than repeated addition. It may seem trivial, but (4 + 4 + 4) is different than (4 * 3). They result in the same quantity, but they are operationally different. In the repeated addition there is no three.
- If a teacher wants to give each, of their 8 students, 2 mini donuts, how many mini-donuts will they need?
- Draw 8 students and put two donuts with each student and count them. 16 or
- Skip count by two for each of 8 fingers. 2, 4, 6, 8, 10, 12, 14, 16
Unitize as requirement for multiplication & place value
In the middle elementary grades learners begin to unitize.
To do so, they must simultaneously understand a group represents two different values.
- Two groups of four
- Represents two single groups;
- (* * * *) (* * * *) and
- Two equal groups of four
- Total of eight.
They are able to switch from one to the other, easily recognizing the equality of the values and the interchangeability of factors as single units or equal groups of those units.
In other words, they can represent five nickels as five nickels and 25 cents, simultaneously being equal. Young learners have difficulty with this. They may say they are equal, but will argue they are not the same, as one is nickels and the other pennies.
Multiples of ten and place value
Children who can skip count by 10. May use it to compose and decompose numbers as they do with the operations of addition and subtraction. However, to have a good understanding of place value they must be able to unitize. Recognize that tens are simultaneously one ten and ten ones. Similarly with 100's and 1000's.
Young children demonstrate their lack of unitizing when they are given numbers and asked to explain the place value of the digits. For example:
Provide a young learner with a group of objects to count (beans, cubes, tokens). Select a number between 23 - 46) Ask the learner to count out a number of objects: 24. When they finish, ask them to write the total (24) on a piece of paper. Then point to the two and the four and ask them to show you what the 2 and 4 represent (in 24) in counters. Or ask them to show you what objects go with the 2 and what objects go with the 4.
I have observed hundreds of young children do this activity and young children: When given 24 objects and asked to show what the 2 and 4 represent in 24. Will put two of the objects by the 2 and four by the 4. When asked what about the other 18, they will either slide them aside or look befuddled.
Older children will easily unitize, know, and explain the 2 is 2 tens while saying it can also be, at the same time (simultaneously), 20 tiles, or 20 units/ ones, and the four represents or stands for 4 tiles. Together 24 tiles.
Learners who understand place value will have a good sense of number values. They easily round numbers to multiples of ten and can count forward and backward by tens and hundreds starting with any number. They know multiples of ten include 10 * 10, and maybe 10 * 100.
These learners will easily unitize, know, and explain the 2 is two tens while saying it can also be, at the same time (simultaneously), 20 tiles, or 20 units/ ones and the four stands for 4 tiles. Together 24 tiles.
Being able to unitize, middle grade students understand the equality of a product to the relationship of the factors. This relationship can then be used to explain the inverse relationship between multiplication and division. A powerful tool in problem solving.
- If we know a part and the whole we can find the other part and if we know the parts we can figure the whole.
This relationship must be understood efficiently and quickly to be able use the basic facts for solving problems requiring both operations of multiplication and division.
When learners can unitize, they are able to represent multiplication and division in additional ways. For example:
- 9 * 30
- 9 * 30 decompose
- 9 * 3 * 10 associate 9 & 3
- (9 * 3) * 10 multiply
- 27 * 10; 270
- 5 * 18
- 5 * 18; think of 10 * 18 as 1/2 of 180
- 90
- 5 * 18
- 5 * 18 factor 18
- 5 * (2 * 9) associative property
- (5 * 2) * 9 multiply
- 10 * 9 multiply; 90
Representations for multiplication and division
Multiplication
- Iteration of equal groups. A correspondence between two (or more) equal sets of objects. Visualized concretely by young children. Two crackers for each piece of cheese. Five players for each team. As children develop, this becomes unitizing a simultaneous relationship between a unit and a group that interates to combine in a product.
- Measurement of like units, linear, area, volume. Results in a product that is something different than the factors (square feet is the product of linear feet, cubic cm...).
- Grids, arrays, & matrices
- Combinations and Cartesian products
- Trees
- Multiples and factors: Product is the result of a factor times a factor. 4 (factor) * 3 (factor) = 12 (product)
See also development
Iteration of equal groups
Most people begin with a representation of multiplication as repeated addition. It is easy to visualize and works well with problems where equal groups of whole numbers are recognized. However, with fractions, decimals, problems with area, volume, arrays, grids, matrices, combinations, Cartesian products, or trees, the operation of multiplication is not as obvious. Therefore, it is important to introduce learners to other models or representations.
Use story problems to solve and justify with a diagram, model, chart, and represent with symbols.
- Three children each want 5 cookies. How many cookies do they want?
- How many ears in groups of students (1-10)?
- There are ten kids on the playground that want to swing.
- There are two swings how many groups would be swinging?
- How many leaves on groups of three leaf clovers? (1-10)?
- Pizza party so that each person gets 4 pieces of pizza.
- How many slices will we need (1-10)?
- How many ways can you group ____
- How many people can sit at two square tables? Three ___, Four ...
- How about a hexagon table? Two ___, Three ___, Four ...
Measurement
The difference between representing addition and multiplication with measurement distinguishes the difference between the two operations, which can be hidden when multiplication is thought of as repeated addition. However, examples that use measurement can show simple concrete comparisons for students after they conceptualize standard units, area, and volume:
- Iterating linear measurement:
- 6 feet four times. 6 feet + 6 feet + 6 feet + 6 feet; 24 feet
- Multiply area:
- 6 feet by 4 feet: 6 feet * 4 feet; 24 square feet
- Multiply volume:
- 6 feet by 4 feet by 3 feet: 6 feet * 4 feet * 3 feet; 72 cubic feet
For more see also measurement
Grids, arrays, & matrices
 Grids, arrays, and matrices are similar in their visual shape of tiled squares.
Grids, arrays, and matrices are similar in their visual shape of tiled squares.
Young learners first experience these structures with blocks and tiles.
When they are able to count, a good experience is to have them count the blocks or tiles and let them begin to construct a relationship between the number of blocks or tiles in columns, rows, and an  entire array.
entire array.
One of the first patterns they will recognize, is usually square numbers: 4, 9, 16, 25, ...
It is beneficial, when learners make or observe these square arrangements, to talk about square numbers and how the pattern can represent a square number.
Matrix or matrices (plural) is a rectangular array (includes square) of numbers, symbols, or expressions, arranged in rows and columns that represent an association or function. Probably, the first experience young learners will have with them is in a basic fact table.
Early experiences with blocks, tiles, grids, and arrays provides a background for learners to use to construct mathematical ideas, in addition to multiplication and division. 
When students experience grids and arrays. It is helpful to define rows as horizontal and columns as vertical and to use rows for groups, columns as the number of items in each group. Each cell represents an item and the entire array or grid represent all groups and items.
Questions to ask, include:
- How many groups? 4
- How many objects in each group? 3
- How many all together? 12
- How many rows?
- How many columns?
- How many objects in one row?
- How many objects in all rows?
- How many objects in one column?
- How many objects in all the columns?
- How many objects in two row?
How many objects in two columns?
Area models are difficult for students to construct (see also representation). Grids can be drawn for them or given to them along with practice sessions to help them develop skill in making them. Some construction problems are:
- Count around one side and down the middle.
- Struggle to draw straight lines when making a grid. Many times the number of lines is wrong or not to scale.
- Have trouble drawing the grid even with a ruler.
- Have trouble drawing the grid on graph paper.
- Don't understand how the rows and columns are related.
- Count the rows and columns twice.
- Think the corners are counted twice.
- Takes time to see that each square is in a row and column simultaneously.
- Draw 12 lines for 12 squares and end up with 11.
Sample script:
Tell. Make a 3 x 4 grid. 
- Ask. How many rows (horizontal)?4
- How many columns (vertical)? 3
- How many squares? 12
- How many squares in two columns? 8
- How many squares in two rows? 6
- Ask. What a 2 x 30 grid would look like? long short …
- How does it compare to the 2 x 3 grid?
- How many 2 x 3 grids are in the 2 x 30 grid?
- How do you know?
- What would it look like?
- Can you draw it?
- What about 4 x 4 and 4 x 40?
- What about 4 x 39? Decompose and use distributive property. (4 x 30) + (4 x 9)
When learners can use a two dimensional array fairly well, then provide problems for three dimensional arrays.
These experiences prepare learners to use these models for multi digit multiplication, develop and understand multiplication algorithms, algebra multiplication and factorization as demonstrated in this sequence.
Sample plan for multiplication with rectangles, arrays, ...
These are difficult relationships and take much time for students to learn. However, it is essential they do if they are to understand these operations and for algebraic reasoning.
Arrays to show the relationship of multiplication and division
Arrays can help learners understand the relationship of division to multiplication
Give different groups of students one of the following problems to demonstrate with an array, then share and discuss the similarities and differences.
Division:
48 / 12; 4
48 / 6; 8
48 / 3; 16
48 / 2; 24
48 / 1.5; 32
Multiplication:
2 * 24; 48
4 * 12; 48
8 * 6; 48
16 * 3; 48
32 * 1.5; 48
Cartesian
A two dimensional Cartesian coordinate system is a rectangular array or grid with each cell or intersection defined as an ordered pair.
Combinations, permutations, trees, and hierarchical models
Combinations are the number of possible arrangements that a collection of items can be arranged without any condition on the order of selection.
- How many hand shakes would there be if 16 people all shook each others hands?
- If 12 people played checkers with 26 people how many games would be played altogether.
- How many different outfits can be created with 7 shirts and 4 pants?
- Two spinners have three numbers on each spinner, how many combinations of spins are there?

Multiples, facts, and factors
Representations for multiples and factors can be represented by all of the representations described, which can be concrete or symbolic as with factor trees, fact tables, and lists of multiples.
Using multiples of 10
Children who can skip count by 10. May use it to compose and decompose numbers as they do with the operations of addition and subtraction. However, to have a good understanding of multiplication they must be able to unitize. Recognize that tens are simultaneously one ten and ten ones. Similarly with 100's and 1000's.
Multiplication facts and factors are important and become more so in more advanced mathematics. However, since most younger students think of multiplication and division as a correspondence and operate on it with repeated addition and subtraction, it's reasonable to guide their develop of more advanced mental strategies that go beyond the use of repeated addition to include other solutions. Research supports not only teaching facts, but suggest it is beneficial for learners to experience sequences of problems to learn a variety of mental strategies as with addition and subtraction instead of only teaching a traditional algorithms with a lot of drill and practice. Sequences of problems enables learners to invent their own algorithms and additionally improves their number sense, problem solving abilities, and abilities to meaningfully construct multiplication facts with addition and other strategies and eventually learn the basic facts along with a variety of ways to solve multiplication and division problems.
The following explores the power of using factors in the operation of multiplication
Sample
- 9 * 30; use factors of ten and commutative property
- 9 * (3 * 10)
- (9 * 3) * 10
- 27 * 10 ; 270
Sample
- 15 * 18; use factors and commutative property
- 15 * (2 * 9)
- (15 * 2) * 9
- 30 * 9; 270
Sample
- 5 * 18; use factors of ten and commutative property
- think of using tens and adjusting
- (10 * 18), which is (2* 5) * 18; 180
- and 1/2 of 180; 90
See also fractions and multiplication
In addition to using addition and subtraction strategies to solve multiplication and division problems, they can explore and learn multiplication strategies.
Types of division
I find division, the most difficult operation to understand, so if you do too, hang in their until you figure out the following ideas and make them yours.
As noted earlier: division is more complicated than multiplication. It has a dividend divided by the divisor that results in the quotient and sometimes a remainder.
That sentence alone is complicated so let's review the ways division problems are interpreted when people first meet them. Let's create a background for division problems. Suppose a florist mixes flowers with other items to make arrangements. They use some flowers for each arrangement and put them in a container, usually a vase. The following two questions could be given to students as division problems.
A florist usually uses 7 flowers in an arrangement. They have 42 flowers, how many arrangements can they make?
A florist has 42 flowers to arrange in 6 vases for a client. How many flowers would they put in each vase?
In the first problem we know the size of a group and can use that amount as a measure to perform the operation. While, we may call it division, most young learners will use the measure of seven and visualize groups of seven flowers being added until they get to 42. Occasionally one might focus on 42 and subtract a measure of seven to visualize putting seven flowers at a time into vases until all the flowers are used.
If we put this example into mathematical language of division it would be:
42 (dividend or something to divide) / 7 (divisor or number to divide) = 6 (quotient or result of division)
Therefore, this type of division problem is called measurement or quotitive.
In the second problem the size of the group, or amount of flowers in a vase is not known. Young learners ask, what part of the 42 should be put into each vase and use trial and error, or guess and check, to find out. In doing this they visualize partitioning 42 with a one to one correspondence or fair shares like dealing cards into 6 equal groups.
Therefore, this type of problem is called distributive, dealing, and partitive.
Let's look at these in more detail.
Division as measuring, quotitive
Young children see division as a correspondance of values.
For example: To find, how many objects are needed to share in equal amounts according to a certain correspondance. If I have 12 boxes and can stack them three high, how many stacks can I make? The correpsondance will be three boxes for each stack. Represented by division as 12 / 3.
Young children will use the three as a measure and iterate with addition to find how many stacks can be made. 3 + 3 + 3 + 3; 12
Even when a person defines division as repeated subraction, they will still be more likely to use addition to solve these problems, rather than subtraction, 12 - 3 - 3 - 3 - 3.
Sample
- If a teacher has 16 pencils they want to give to their 8 students, how many pencils will each get?
- Draw 8 students and put two pencils with each student and count them. 16 or
- Skip count by two for each of 8 fingers. 2, 4, 6, 8, 10, 12, 14, 16
As students get older, they will recognize problems as division, but mostly solve them with addition and occasionally with subtraction.
Quotient is the result obtained by dividing one quantity (dividend) by another (divisor).
Problem
- If I want to put 28
donuts (dividend) on platters and I want 7 donuts (divisor) on each platter, how many platters
(quotient) are needed?
- How many groups of seven can be made with twenty-eight?
- I have $15 to buy cartons of water and each carton cost $3, how many cartons can I buy?
- How many $3 cartons does it take to spend $15?
Summary
Measurement or quotitive problems fit the pattern:
- How many groups of __ can be made with ___ .
- The size of the groups is specified and the number of groups is unknown.
- Measurement: how many units of a group is in the total number?
- Repeatedly add the number in a group or occasionally repeatedly subtract how many in a group from the total number.
Division as distributing, dealing, or partitive
In distributive or partitive division the size of the group learners would use as a measure, is not known. So young children find this unknown amount, how many objects each person would get, or part of a total of a total amount to be shared, with the total amount known, by distributing small amounts equally into groups, or units, until the total amount is distributed.
A class has 55 cookies and 18 students, how many will each get?
Students start by distributing (dealing out) 1 or 2 cookies for each student and repeat until they run out of cookies. Or they may start with a larger number and run out. Needing to start again with a smaller amount. The process of distributing, for young students, is trial and error not systematic.
I have twenty-one beads and want to use all the beads to make three bracelets, how many beads can I put on each bracelet? (21 / 3)
This involves finding, how many in the group (part of total), when the number of groups are known (3) and the size of the groups is not known (7).
Children begin with a build up strategy and focus on finding the unknown number (7), rather than focusing simultaneously on what numbers might be in one part if there are three parts. This is what makes distributive or partitive problems difficult for learners who haven't developed the ability to unitize what is to be distributed.
In measurement or quotitive problems, the measurement, what to count, is known so it is easier to unitize. However, in partitive problems the value is not known so learners use trial and error, to find it. To do this most children are more confident with a distributing or dealing strategy, because they relate it to a well understood strategy of one to one correspondence, which is easy to visualize as a fair share, one for me one for you strategy.
They do not yet see the number of groups as a unit to use to find what quantity to distribute or deal out, or partition into the groups to make them equal or have fair shares.
Since they have frequently experienced one for me one for you strategy or dealing cards as a one to one relationship, they are more confident to use an equal distribution to find the size of the groups. However, even if they concretely distribute the number of items (dividend) to all the groups, they are not confident in the process and will count them to check for sure that each group has the same number.
Learners must understand the relationships of the groups as part whole relationships. And the numbers in a group and that group are both one whole unit simultaneously (unitize). These big ideas need to be constructed to really understand the operation of division. More in moving toward unitizing division later.
Some people tell students, division is repeated subtraction. This is an incomplete analysis and may hinder a learner's ability to construct an understanding of the part/whole relationships in multiplication and division. Mostly, because as we have shown learners use addition to solve division problems.
Summary
- Partitive is to find the size of one part (unit) of a divisor.
- If a whole has ____ parts and the whole is ____, how much is each part?
- Distributive is to find the number of groups and their size.
- If ___ is distributed to ___ groups, how much is in each group?
Mixed sample problems
Review a problem and decide how young learners would solve it and what type of division it would be:
Sample 1
I have $12; if socks cost $3 a pair, how many pairs can I buy?
Is it measurement (quotitive) or distributive (dealing, partitive)?
Measurement - the total amount ($12) and the size of a group ($3) is known. Therefore, the cost of a pair of socks is used to measure how many groups or pairs of socks would equal the total amount. Students will either use repeated addition or subtraction. It would be visualized as adding $3 up to $12 or subtracting $3 from $12 for each $3 spent till all is spent.
Sample 2
Socks are on sale at 3 pairs for $12; how much is one pair?
Is it measurement (quotitive) or distributive (dealing, partitive)?
Distributive (dealing, partitive) - find the size of a part. Distributive - You know the total size ($12) and total number of groups (3). Need to find how the money ($12) is distributed among (or shared or dealt out to) the groups for each of 3 pairs of socks.
Both sample 1 and sample 2 divide 12 by 3. However, to young people they are very different problems, which they solve differently.
In the first, it makes sense to measure how many $3 there are in $12. To take $3 and then $3 more, until you get to $12. They don't subtract, they add. It doesn't make sense to distribute or subtract 3 pairs from $12 to solve it as partitive.
In distributive (dealing or partitive) they use trial and error and distribute or share or deal out $ strategy to distribute dollars to each of three pairs.
They solve both problems very differently. How do they discover that both of these kinds of problems are division?
Moving toward unitizing division
One way to help learners unitize is to give them two similar problems. In a classroom situation you can give one to half the students and the other to the other half. Ask them to solve the problem and draw a diagram to support their solution.
Sample A
If a hotel has 240 rooms, 24 rooms per floor, how many floors?
Sample B
If a hotel has 240 rooms and 24 floors, how many rooms on a floor?
- Students will do each problem differently.
- Have them share their solutions.
- Discuss:
- Ask. What is the same? the numbers are the same
- What is different? Have them use their diagram as a model of each hotel to show the floors, rooms per floor, and total rooms in each hotel. 10 x 24 and 24 x 10.
- Mention: Multiplication being commutative.
- Ask. How does multiplication relate to division?
- Ask. How does that relate to division?
Follow these problems with others that also bring the two types together into one problem:
Sample
The teacher bought 186 pencils and wanted to put them on six tables, how many would they put at a table? They also said, the pencils came in a box of six, how many boxes did they buy?
- In the first part, students will probably distribute (deal, partitive) pencils among the six tables. 31 per table
- In the second part, they will use a box of six as a unit and measure (quotitive). 31 boxes
Another problem, such as the following, may help students unitize groups.
Sample
How many tables would be needed if 81 guests are invited and 6 are to be sat at a table.
- Have students discuss their solutions and explain why they believe they are accurate.
- Hopefully they will drew tables with 6 (unitize) and count on until 81.
- Some may figure 6 * 10 = 60 (unitize) and 4 more would be needed. 60 + (4 x 6) = 60 + 24.
Another way to help students unitize is to create problems with groups or objects that aren't easily partitioned. The following is an example that does this and also encourages the use of the distributive property.
Sample
If you are going to serve each person a glass of lemonade and each pitcher holds seven glasses, how many pitchers are needed if you are expecting 300 people?
Strategies for multiplication & division
Visualize or diagram problems .....
Use diagrams to show: equal groups to iterate, drawings to show measurements linear, area, volume, and more; grids, arrays, & matrices, combinations or Cartesian products, trees, multiples and factors.
Iterating equal groups
- Counting by ones
- (2 * 4);
- (1, 2, 3, 4) + (5, 6, 7, 8); 8
- Skip counting
- 2, 4, 6, 8, 10, 12, 14, 16, 18 20 ...
- 3, 6, 9, 12, 15, 18, 21, ...
- 5, 10, 15, 20, 25, ...
- Repeated addition
- (3 * 3);
- 3, 6, 9; 9
- Doubling is associated with the associative property. However, it is important enough to include separately.
- 2 * 12; double 12; 24
- 4 * 12; double 12 twice; 24; 48
- 2 * 24; double 24; 48
- 4 * 24; double twice; 48; 96
- 8 * 24; double three times 8 is (2 * 2 * 2); 48; 96; 192
- 8 * 12; double three times
- 24 * 2 any of the following; (48 * 1), (24 * 2), (12 * 4), (6 * 8), (3 * 16), (1 * 48)
- 4 * 24, any of the following; 2 * 48, 8 * 12, 16 * 6, 32 * 3
- practice doubling numbers; 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ...
- Egyptians multiplied by doubling
- 28 x 12
- 1 x 28; 28
- 2 x 28; 56
- 4 x 28; 112
- 8 x 28; 224
- 4 + 8 is 12, Therefore
- 112 + 224 is 336
- Russian peasants used a halving and doubling algorithm
- 28 x 12; take half of 28 and double 12
- 14, 24; again, half and double
- 7, 48 select all the odds and their doubles,
- 7, 48 take half, forget the remainder, and double
- 3, 96 take half, forget the remainder, and double, until you get to one
- 1, 192 one
- Add all the odd doubles
- 48 + 96 + 192; 336
- Halving
- 1024, 512, 256, 128, 64, 32, 16, 8, 4, 2
- Doubling and halving
- 5 * 6; double five and half 6
- 10 * 3; 30
- 50 x 42, (100 x 42 = 4200), 4200/2 = 2100 or 100 * 21 = 2100
- 3 1/2 * 14; double 3 1/2 and half 14
- 7 x 7; 49
- 5 * 6; double five and half 6
- Halving and doubling
- 4 * 3 take half of 4 and double 3
- 2 * 6; 12
- Unitize units - separates units into groups. Can simultaneously consider the number of objects and groups as two subgroups of objects for the number of groups (distributive property).
- Unitize five groups of eight (5 * 8) and regroup as five groups of five & five groups three
- 5 * 8
- (5 * 5) + (5 * 3)
- 25 + 15; 40
Use multiples, factors, primes, and composites
Multiples, factors, multiplication and division facts are often memorized without an accurate representation (equal groups, square, array, grid, tree ...). Without an accurate representation learners will often visualize the factors placed in a progression of numbers moving farther away, with the smaller factor being closest, followed by the next factor, and the product being much farther away. This representation encourages counting singly or by skip counting in different amounts two, three, five, ten; being the most common. Young children, if they have learned to skip count, will discover different multiples to use as landmarks. These representations are not a clearly defined numberline and as the numbers become greater the accuracy is decreased.
Other representations, which are not spatial, can be used as neumonic devices to assist memory. Memorize by chaining values as sing song, as in skip counting (2, 4, 6, 8, ...), rhymes (six times eight is forty-eight or just six eight forty-eight), basic fact tables, and factor trees are examples.
The more we explore multiples and factors the easier they are to remember.
Exploration can include recognizing patterns, seeing how different numbers can be composed and decomposed to assist learning and memorizing factors and multiples. More exploration examples:
- Explore basic fact tables and strategies to compose and decompose the facts to assist in memorizing or recalling multiplication facts
- Explore multiples
- Factors for the First 50 or 100 Numbers - plans & work sheets
- Primes and the fundamental theory of arithmetic (FTA)
Know both concretely and abstraxtly or memorized?
Use properties
Distributive property
- 5 * 8 distributed as
- (5 * 5) + (5 * 3)
- 25 + 15; 40
- 7 * 8
- (5 * 8) + (2 * 8); 56 or
- (8 * 8) - (1 * 8); 56
- 9 * 8; think 10
- (10 * 8) - (1 * 8); 72
Commutative property for multiplication. Move factors. (factor x factor = product)
- 7 * 8 is the same as 8 * 7 commuted (moved)
- 8 * 5; same as 5 * 8 commuted (moved)
Associative property for multiplication
- Using the associative property is often coupled with the distributive property
- 30 * 6 use the distributive property
- 3 * 10 * 6 associate ten and six
- 3 * (10 * 6) add ten six times
- 3 * 60 take sixty three times; 180,
- Or 30 * 6 use the distributive property
- 3 * 10 * 6 associate ten and six
- (3 * 6) * 10 multiply three times six
- 18 * 10 take eighteen time ten; 180,
- Create a rectangle model to show
- 3 * 10 * 6; 3 * 6 * 10; are the same as 30 * 6
- 70 x 8 ?
- 30 * 6 use the distributive property
- 5 * 9 * 2 associate 5 & 2
- 9 * (5 * 2);
- 9 * 10; 90
Developing multiplication & division algorithms
Young learners create their own algorithms. When they do they usually work from left to right starting with tens and use the distributive property. This is backwards from the traditional algorithm (right to left). Rectangles & arrays can help learners visualize multiplication and invent strategies for multipication and division that will include traditional algorithms along with knowing what strategies are best used for different types of problems.
Constance Kamii's research has led her to insist: teaching children algorithms is harmful to their mathematical development. Some of her reasons include:
- Children want to do multiplication from left to right - largest to smallest (algorithm is opposite).
- In division they want to go from smallest to largest, right to left (algorithm is opposite).
- Children have to give up their sense making in order to perform the algorithm.
- It hinders children's ability to construct understanding of the distributive property of multiplication.
- Doesn't encourage understanding of place value.
- Develops dependency on the spatial arrangement of the number's digits on paper.
- Worst of all it causes children to see themselves as proficient users of someone else's mathematics, not as mathematicians themselves.
Most strategies learners create are inefficient. Therefore, sharing different strategies is needed to help students create efficient algorithms. Mathematics in the City looked at how to help learners facilitate their development of efficient computation strategies, which require a deep understanding of number sense and operations that build on children's own constructions.
Presenting students with sequences of problems to solve and discuss can facilitate the development of more efficient ways to solve problems.
Sample sequence of problems
- 5 x 6
discussion
- I know 6 x 6 is 36 and I subtracted 6 to get 30
- I know 10 x 6 is 60 and I halved it and got 30.
- 30 x 6 discussion
- I know 30 + 30 is 60, then 60 + 60 + 60; 180
- 35 x 6 discussion
- hopefully they will use previous solutions and the distributive property. If not, demonstrate
- 35 * 6
- (30 * 6) + (5 * 6)
- 180 + 30; 210
- If students understand, draw and label a rectangle model
- Decide what to do next:
- 40 * 7 then 2 * 7 then 42 * 7 to get to the of the distributive property (40 * 7)+ (2 * 7).
- 5 * 6 then 30 * 6 then 35 * 6 to get to the of the distributive property (30 x 6) + (5 x 6).
- If students understand, draw and label a rectangle model
- Ready to start with problems like 25 * 4 to have students work in pairs to solve and document in their journals by writing the solutions they used and drawing rectangles or arrays. If students haven't had numerous experiences with blocks or array models, it may be helpful to have them use concrete objects before drawing. They can use Cuisenaire rods, cubes and
squares, tiles, grid paper, and Multilink cubes. With sufficient experiences, they should be able to visualize a mental model.
- 25 * 9
- 26 * 9
- 35 * 7
- 46 * 5
- Ask if they can invent a rule. Decompose one factor into tens and ones and multiply each part by the other factor.
- Have them create their own problem to demonstrate their rule.
- Continue with more as necessary.
- Use the distributive property with tens and adjust
- 49 * 7 adjust tens
- (50 * 7) - 7
- 48 * 7
- 51 * 7
- 98 x 32 = (100 x 32) - (64)
- Create a model, name the strategy.
- 37 x 84 = (30 x 80) + (7 x 80) + (30 x 4) + (7 x 4)
- Create a model, name the strategy. E.g. worse case strategy
When learners are proficient with multiplication of one digit with two digit numbers and understand that all digits need to operate on each other, they can be introduced to the multiplication of two digit numbers so they can discover that multiplication of two digit numbers also requires numbers in each place operate on each number in all the other places.
- 23 * 34 decompose
- (20 * 30) + (20 * 4) + (3 * 30) + (3 * 4)
- 600 + 80 + 90 + 12; 782
This is one way multiplication is unlike addition and learners who conceptualize multiplication only as repeated addition never fully realize the potential of multiplication. This presents problems as students move further into higher branches of mathematics: specifically algebra and beyond. See area models to help learners represent this idea and connect it to algebra.
Different models can be used to represent these ideas, However, while they help provide concrete experiences for multiplication, students really need multiple experiences as they struggle with what multiplication is and how it is and isn't related to addition. Likewise, they will need to struggle with division.
Models related to multiplication and division
Multiply 18 x 23.
Which of the following strategies did you use?
- 18 * 23
- 20 * 23 - (2 * 23)
- 460 - 46; 414
- 18 * 23
- (18 * 20) + (18 * 3)
- 360 + 54; 414
- 18 * 23
- (3 * 8) + (3 * 10) + (20 * 8) + (20 * 10)
- 24 + 30 + 160 + 200; 414
The last one represents the traditional algorithm. Which is easier?
Now get a piece of graph paper, draw a 20 X 30 grid, and show where the numbers in the traditional algorithm came from.
Check your diagram with this grid or square model and see how it connects to algebra factors and binomials, ... How the traditonal algorithm works and why understanding it is critical to understand algebra E.g. (x + 1) (x + 1)
Arrays -
Lesson plan for multiplication with arrays
Problems people have with arrays:
View as one directional (count all squares in a one directional path).
View as a set of rows or columns, but not both.
View as both a set of rows and columns but not both simultaneously,
Can't see how corners can be both a row and column.
Can view corner squares, and others, as being both a row and column
Once students have constructed unitizing they can use multiplication to solve division problems
Multiplication by .1, .01, .001
Multiplication and Division of Whole Numbers Concepts for Computation/Algorithms
Division algorithm
To understand the division algorithm it is necessary to understand the distributive property of multiplication along with the relationships of factors and multiples.
For example: divide 275 / 25 with a traditional algorithm you use (25 * 10) + (25 * 1)
The distributive property can be used to decompose the numbers without using the exact factors of the divisor ( 25 * 11) or with the use of place value as done with the long division algorithm. Sometimes it will be easier to decompose with to friendly factors:
Sample problem
- 275 / 25 think I know multiples of quarters 25, 50, 75, 100 so use distributive property
- (200 + 75) / 25
- (200 / 25) + (75 / 25) 4 * 25 is 100 ∴ 8 * 25 is 200 and three quarters is 75 cents
- 8 + 3; 11
Or
- 275 / 25 know four quarters is $3.00 or 300 ∴ 25 * 12 is 300
- 300 - 25 is 275 if 12 * 25 is 300, then 11 * 25 is 275 or
- 275 / 25; 11
Use arrays, matrices, grids, base ten blocks, Cuisenaire ..., Multilink cubes, Meter stick, Money… to show these representations
1224/24, Use halving 612/12, 306/6, then 51
Or make it friendly: 1200/24 + 24/24, then halve to get 600/12 and divide to get 50,
That makes 50 + 24/24 = 50+1 = 51 Or halving 1224/24, 612/12, 306/6, 153/3, then divided by three and got 51.
Sources
Fosnot, Catherine Twomey; & Dolk, Marten. (2001). Young Mathematicians at Work: Constructing Multiplication and Division. Portsmouth, NH: Heinemann.
