Earth's Circumference, Eratosthenes, Astronomy, Solstices, Equinoxes, Latitude, Science, and Math Activity
Eratosthene's
Eratosthenes, a Greek geographer (about 276 to 194 BCE), made a surprisingly accurate estimate of the Earth's circumference.
In the great library in Alexandria, Egypt he read that there was a deep vertical well near Syene, in southern Egypt, that was entirely lit to the bottom of the well by the sun at noon once a year: summer solstice. Eratosthenes understood if the sun is directly overhead, its rays would shin straight down into the well and lite the bottom.
Solstice is either of two times in a year, the Summer Solstice and the Winter Solstice. A solstice is when the sun is at its highest or lowest point in the sky at noon. Which makes the longest and shortest days (about June 22 and December 20). Caused by the Sun's motion being the longest or shortest path across the sky.
The Tropic of Cancer is north of the Equator at 23.4372° latitude. It is the latitude where once a year the sun is directly overhead on the Summer Solstice.
The Tropic of Capricorn is south of the Equator at -23.4372° latitude. It is the latitude where once a year the sun is directly overhead on the Winter Solstice.
Equinox is the day (twice each year) when the sun crosses the celestial equator, when day and night are of equal length (about September 22 and March 20).
Eratosthenes, understood the movement of the Sun across the sky. He knew in Alexandria, Egypt the sun was not directly overhead at noon on summer solstice because vertical objects there cast a shadow. He knew that Alexandria was 5000 stadias almost due north of Syene, Egypt. And he understood enough geometry to reason he could use this information to calculate the circumference of the Earth.
Assumptions:
- He assumed: the Earth was round (sorry Columbus).
- The sun's rays traveled in a straight line. and
- The rays both places were essentially parallel.
Data:
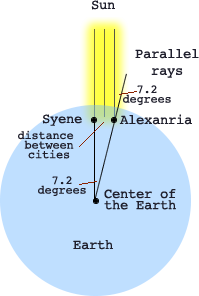
He set up a vertical post at Alexandria and measured the angle of its shadow at summer solstice (7.2 degrees), when the well at Syene was completely sunlit, which meant the sun was vertically over the well.
Reasoning:
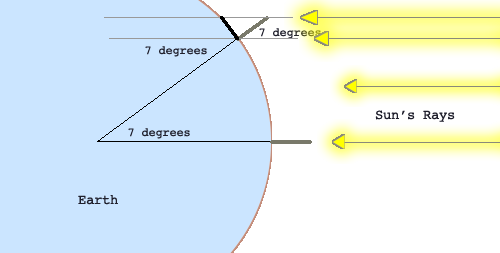
- From geometry, Eratosthenes knew, the angle of the shadow at Syene equaled the angle at the earth's center between Syene and Alexandria. A line crossing parallel lines will have the same angles.
- The arc of an angle this size was, therefore, 1/50 of a circle (360° / 7.2° ≈ 50). Based on 360° assumption of a round earth.
- The distance between Syene and Alexandria was 5000 stadias.
- So he multiplied 5000 by 50 to find the Earth's circumference.
- His result, 250,000 stadias (about 46 250 km) is quite close to modern measurements (40 075 km at the equator).
Source Investigating the Earth, AGI, 1970, Chapter 3, p. 66.
The formula Eratosthenes used:
(360° / shadow angle of vertical stick) * distance from Syene to Alexandria = Circumference of the Earth
Formula you can use to calculate circumference of the Earth.
(360° / shadow angle of vertical stick) * distance from Syene = Circumference of the Earth
Syene is located on or near the Tropic of Cancer (23.5° N), where the Sun would be overhead on the Summer Solstice.
- The Sun is directly overhead of the Tropic of Cancer (23.5° N) on Summer solstice,
- Overhead of the Tropic of Capricorn (23.5° S) on Winter Solstice
- Overhead of the Equator (0° N) on Spring and Fall and Equinoxes.
Use these ideas to determine the Earth's circumference.
- On the Summer Solstice place a vertical stick into the ground.
- When the sun reaches it's highest vertical assent for the day (solar noon therefore the shadow length will be the shortest), measure the angle of the shadow (shadow angle of a vertical stick).
(360° / shadow angle of vertical stick) * distance from Tropic of Cancer = Circumference of the Earth
On the equinox, the vertical rays of the sun are directly over the equator. How would you calculate the circumference of the Earth using the same method during an equinox?
How about sharing shadow angle measurement with others around the real globe. Contact others that would be willing to collect the same data and exchange it possibly using the following format.
Date of measurement ____________
Your measurement of the shadow angle ____________ degrees
Your location city ____________________________________
Your location country _________________________________
Your latitude _________________________________________
Your longitude ________________________________________
When you have different sets of data compile them and compare the various locations and angles.
Original idea by Jim Meinke (September 1994) Lakewood High School in Cleveland.