Discussion of multiples, primes, & the fundamental theory of arithmetic (FTA)
Introduction
The following ids a discussion of multiples, common multiples, least common multiple, primes, composites, and factors that leads to discovering the fundamental theory of arithmetic (FTA).
Set up
After exploring multiples and common multiples a learner says:
You can figure out the second common multiple by doubling the least common multiple (LCM).
Then added, "Does it always work?"
When prompted to try to find a counter example, and after awhile they replied.
So far I cannot find a non example of this conjecture.
Do you know of any two numbers where this conjecture does not work???
Let's review what you have so far:
Conjecture: The second common multiple is always a double of the least common multiple (LCM).
Specific examples generated by the student:
Take two numbers. Say 3 and 4.
Find the first common multiple by listing all the multiples for each:
- Common multiples of three: 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, ...
- Common multiples of four: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, ...
Therefore, the first common multiple (LCM) is 12, the second is 24, the third is 36, ...
Therefore, for this example the first common multiple (LCM) is 12 and the second is 24; and 24 is twice 12.
Hence, the question ...
Will the second common multiple (24 in this example) always be twice the first?
Teacher decision time:
- Should I stay with generating multiples for different numbers, compare them, and let the student see how all the examples are multiples of two and hope the ah ha moment will be all second multiples are two times the first, therefore, double. or
- Use prime factorizations to show how the second multiple has the same factors as the first multiple and two. Therefore, as a multiple of two, a double.
An added bonus with the second method is: it can provide an excellent opportunity to introduce the Fundamental Theorem of Mathematics (FTA) as a stronger proof and to provide a wider application for the understanding of multiples, factors, and their relationships.
One way to proceed:
We could find for each multiple in each of the sets of multiples (3 and 4) all the prime factors for each multiple.
My reasoning is that if I can find all the smallest factors that are only primes, then I may be able to show a pattern to generalize for every multiple.
So a list of all the smallest factors (primes) for the first few multiples of each multiple for: three and four.
0
3 - 3
6 - 2, 3
9 - 3, 3
12 - 2, 2, 3
15 - 3, 5
18 - 2, 3, 3,
21 - 3, 7
24 - 2, 2, 2, 3 ---> notice this is exactly the same as the prime factors of 12 * 2 or double. Try some more examples... Can make it infinite?
27 - 3, 3, 3
30 - 2, 3, 5
33 - 3, 11
36 - 2, 2, 3, 3 ---> notice this is exactly the same as the prime factors of 12 * 3 or triple.
0
4 - 2, 2
8 - 2, 2, 2
12 - 2, 2, 3 ---> notice....
16 - 2, 2, 2, 2
20 - 2, 2, 5
24 - 2, 2, 2, 3 ---> notice...
28 - 2, 2, 7
32 - 2, 2, 2, 2, 2
36 - 2, 2, 3, 3 ---> notice ...
NOW this is where the student might see the pattern and recognize the answer to his or her question.
If they do or don't either way, it is still necessary to complete the next step, and illustrate the Fundamental Theorem of Arithmetic.
To get to that discovery, look at the prime factors for the first 25 whole numbers?
0 - not a prime by definition
1 - not a prime by definition
2 - 2
3 - 3
4 - 2, 2
5 - 5
6 - 2, 3
7 - 7
8 - 2, 2, 2
9 - 3, 3
10 - 2, 5
11 - 11
12 - 2, 2, 3
13 - 13
14 - 2, 7
15 - 3, 5
16 - 2, 2, 2, 2
17 - 17
18 - 2, 3, 3
19 - 19
20 - 2, 2, 5
21 - 3, 7
22 - 2, 11
23 - 23
24 - 2, 2, 2, 3
25 - 5, 5
Okay now, which of the numbers have exactly the same factors?
NONE?
WOW! Every whole number is a product of a unique set of prime numbers. In other words a group of primes has only one product. AND every whole number only has one set of prime numbers that can be used to make that number.
Now. If you are all still with me, put these two ideas together and think of
12 as the group of primes 2, 2, 3.
In order to get the next multiple, of that number, it would have to include another prime factor; and the smallest prime is 2.
Oh, wow!
- 12 = 2 * 2 * 3 and multiply it by the smallest prime
- 2 * 2 * 3 * 2
- and where was something like that seen before?
- 24 = 2 * 2 * 2 * 3
Summary
Let's represent primes to 30 on a number line:
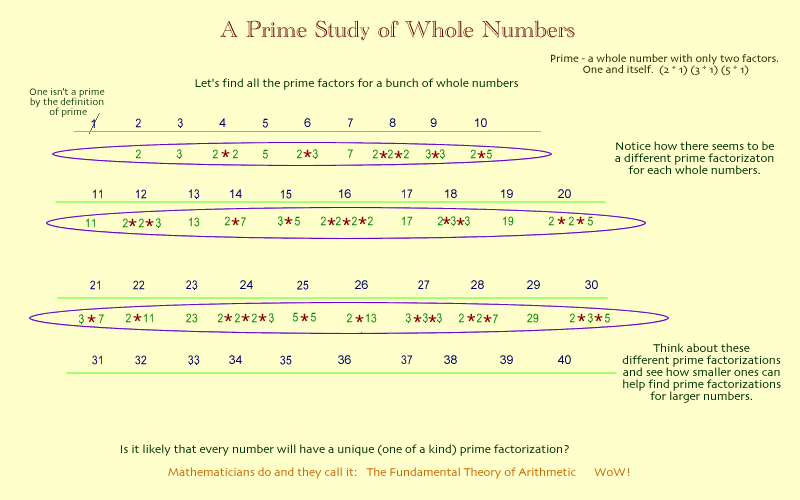
Therefore, if every whole number can be expressed as a unique group of primes, then any whole number (which would include any LCM for any group of numbers) would have as its next multiple one more factor and the smallest factor that it could be is two. SOoo, anyone that wants to find a counterexample that doesn't fit this students conjecture, probably will have a long search.
YES! Wasn't that fun?